题目内容
【题目】如图，正三棱锥A﹣BCD的侧棱长为2，底面BCD的边长为2 
，E，分别为BC，BD的中点，则三棱锥A﹣BEF的外接球的半径R= ， 内切球半径r= ． 
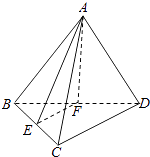
【答案】1；2﹣ 
【解析】解：设三棱锥A﹣BEF的外接球的球心为O，则O在平面BEF上的射影O′为△BEF的中心，
∴BO′= 
× 
= 
∵A到平面BCD的距离为 
= 
，
∴三棱锥A﹣BEF的外接球的半径R= 
=1，
三棱锥A﹣BEF的体积V= 
= 
，
又S= 
+2× 
+ =2+ ，
∴ = （2+ ）r，
∴r=2﹣ ．
所以答案是：1，2﹣ ．
【考点精析】解答此题的关键在于理解球内接多面体的相关知识，掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．
练习册系列答案
相关题目
【题目】某同学在利用“五点法”作函数f（x）=Asin（ωx+）+t（其中A＞0， 
）的图象时，列出了如表格中的部分数据．
x |
|
|
|
|
|
ωx+ | 0 | | π | | 2π |
f（x） | 2 | 6 | 2 | ﹣2 | 2 |
（1）请将表格补充完整，并写出f（x）的解析式．
（2）若 
，求f（x）的最大值与最小值．
【题目】东莞某家具生产厂家根据市场调查分析，决定调整新产品生产方案，准备每周（按40个工时计算）生产书桌、书柜、电脑椅共120张，且书桌至少生产20张．已知生产这些家具每张所需工时和每张产值如表：
家具名称 | 书桌 | 书柜 | 电脑椅 |
工 时 |
|
|
|
产值（千元） | 4 | 3 | 2 |
问每周应生产书桌、书柜、电脑椅各多少张，才能使产值最高？最高产值是多少？（以千元为单位）