Question

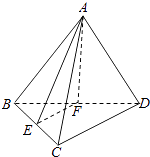
【题目】△ABC中，D为边BC上的一点，BD=33，sinB= ，cos∠ADC= ，求AD．

Answer 1

【答案】解：由cos∠ADC= ＞0，则∠ADC＜ ，
又由知B＜∠ADC可得B＜ ，
由sinB= ，可得cosB= ，
又由cos∠ADC= ，可得sin∠ADC= ．
从而sin∠BAD=sin（∠ADC﹣B）=sin∠ADCcosB﹣cos∠ADCsinB= = ．
由正弦定理得 ，
所以AD= = ．
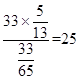【解析】先由cos∠ADC= 确定角ADC的范围，因为∠BAD=∠ADC﹣B所以可求其正弦值，最后由正弦定理可得答案．
【考点精析】解答此题的关键在于理解同角三角函数基本关系的运用的相关知识，掌握同角三角函数的基本关系：；;（3） 倒数关系：，以及对正弦定理的定义的理解，了解正弦定理:．