题目内容
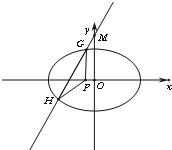
在平面直角坐标系中,N为圆C:(x+1)2+y2=16上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且
•
=0.
(Ⅰ)求动点P表示的曲线E的方程;
(Ⅱ)若曲线E与x轴的交点为A,B,当动点P与A,B不重合时,设直线PA与PB的斜率分别为k1,k2,证明:k1•k2为定值.
| MP |
| DN |
(Ⅰ)求动点P表示的曲线E的方程;
(Ⅱ)若曲线E与x轴的交点为A,B,当动点P与A,B不重合时,设直线PA与PB的斜率分别为k1,k2,证明:k1•k2为定值.
(Ⅰ)由点M是DN的中点,
•
=0,可知PM垂直平分DN.
所以|PN|=|PD|,
又|PC|+|PN|=|CN|,所以|PC|+|PD|=4.
由椭圆定义知,点P的轨迹是以C,D为焦点的椭圆.----------------------(4分)
设椭圆方程为
+
=1(a>b>0).
又2a=4,2c=2,可得a2=4,b2=3.
所以动点P表示的曲线E的方程为
+
=1.----------------------(6分)
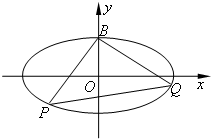
(Ⅱ)证明:易知A(-2,0),B(2,0).
设P(x0,y0)(y0≠0),则
+
=1,即
=3(1-
),
则k1=
,k2=
,----------------------(8分)
即k1•k2=
=
=
=-
,
∴k1•k2为定值-
.-----------------------------------12
| MP |
| DN |
所以|PN|=|PD|,
又|PC|+|PN|=|CN|,所以|PC|+|PD|=4.
由椭圆定义知,点P的轨迹是以C,D为焦点的椭圆.----------------------(4分)
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
又2a=4,2c=2,可得a2=4,b2=3.
所以动点P表示的曲线E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)证明:易知A(-2,0),B(2,0).
设P(x0,y0)(y0≠0),则
| ||
| 4 |
| ||
| 3 |
| y | 20 |
| ||
| 4 |
则k1=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
即k1•k2=
| ||
|
3(1-
| ||||
|
-
| ||||
|
| 3 |
| 4 |
∴k1•k2为定值-
| 3 |
| 4 |

练习册系列答案
相关题目