题目内容

已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，两个焦点分别为F1和F2，椭圆C上一点到F1和F2的距离之和为12．
（Ⅰ）求椭圆C的方程；
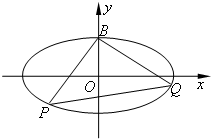
（Ⅱ）设点B是椭圆C的上顶点，点P，Q是椭圆上；异于点B的两点，且PB⊥QB，求证直线PQ经过y轴上一定点．
（Ⅰ）设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的半焦距为c，
则∵椭圆C上一点到F1和F2的距离之和为12，离心率为
3
2
，
∴
2a=12
c
a
=
3
2
，解得
a=6
c=3
3
，
∴b2=a2-c2=9．
∴所求椭圆C的方程为：
x2
36
+
y2
9
=1．…（4分）
（Ⅱ）显然直线PQ的斜率存在，设直线PQ的方程为y=kx+b
联立方程组
y=kx+b
x2
36
+
y2
9
=1
，消去y整理得（1+4k2）x2+8kbx+4b2-36=0．
设P（x1，y1），Q（x2，y2），则x1+x2=-
8kb
4k2+1
，x1x2=
4b2-36
4k2+1
．
∴y1+y2=k（x1+x2）+2b=
2b
4k2+1
，y1y2=
b2-36k2
4k2+1
…（8分）
∵PB⊥QB，且
BP
=（x1，y1-3），
BQ
=（x2，y2-3），
∴
BP
•
BQ
=x1x2+（y1-3）（y2-3）=0，
∴
4b2-36
4k2+1
+
b2-36k2
4k2+1
-3•
2b
4k2+1
+9=0
∴5b2-6b-27=0．
解得b=-
9
5
或b=3（舍去）
∴直线PQ经过y轴上一定点（0，-
9
5
）．…（12分）
练习册系列答案
相关题目
已知双曲线C的中心在原点，抛物线y2=2
5
x的焦点是双曲线C的一个焦点，且双曲线经过点(1，
3
)，又知直线l：y=kx+1与双曲线C相交于A、B两点．
（1）求双曲线C的方程；
（2）若
OA
⊥
OB
，求实数k值．
已知直角坐标平面内点A（x，y）到点F1（-1，0）与点F2（1，0）的距离之和为4．
（1）试求点A的轨迹M的方程；
（2）若斜率为
1
2
的直线l与轨迹M交于C、D两点，点P(1，
3
2
)为轨迹M上一点，记直线PC的斜率为k1，直线PD的斜率为k2，试问：k1+k2是否为定值？请证明你的结论．
设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且
AP
=
8
5
PQ
．
（1）求椭圆C的离心率；
（2）若过A、Q、F三点的圆恰好与直线l：x+
3
y+3=0相切，求椭圆C的方程．
已知一条曲线C在y轴右侧，C上每一点到点F（1，0）的距离减去它到y轴距离的差都是1．
（1）求曲线C的方程；
（2）设直线l交曲线C于A，B两点，线段AB的中点为D（2，-1），求直线l的一般式方程．
已知椭圆C的中心在原点，一个焦点为F(0，
2
)，且长轴长与短轴长的比为
2
：1．
（1）求椭圆C的方程；
（2）若椭圆C上在第一象限内的一点P的横坐标为1，过点P作倾斜角互补的两条不同的直线PA，PB分别交椭圆C于另外两点A，B．求证：直线AB的斜率为定值．
如图，已知F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，且椭圆C的离心率e=
1
2
，F1也是抛物线C1：y2=-4x的焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F2的直线l交椭圆C于D，E两点，且2
DF2
=
F2E
，点E关于x轴的对称点为G，求直线GD的方程．
在平面直角坐标系中，N为圆C：（x+1）2+y2=16上的一动点，点D（1，0），点M是DN的中点，点P在线段CN上，且
MP
•
DN
=0．
（Ⅰ）求动点P表示的曲线E的方程；
（Ⅱ）若曲线E与x轴的交点为A，B，当动点P与A，B不重合时，设直线PA与PB的斜率分别为k1，k2，证明：k1•k2为定值．
已知椭圆C的中心在原点，焦点在x轴上，离心率e=
1
2
，一个顶点的坐标为(0，
3
)．
（1）求椭圆C的方程；
（2）椭圆C的左焦点为F，右顶点为A，直线l：y=kx+m与椭圆C相交于M，N两点且
AM
•
AN
=0，试问：是否存在实数λ，使得S△FMN=λS△AMN成立，若存在，求出λ的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网