Question

【题目】已知函数f（x）=x|x﹣a|+x．
（1）当a=3时，求函数f（x）的单调递增区间；
（2）求所有的实数a，使得对任意x∈[1，4]，函数f（x）的图象恒在函数g（x）=x+4图象的下方．

Answer 1

【答案】
（1）解：当a=3时，函数f（x）=x|x﹣a|+x=x|x﹣3|+x=

x≥3时，f（x）=x2﹣2x是增函数，x＜3时，f（x）=4x﹣x2，开口向下，对称轴为：x=2，

∴函数f（x）的单调递增区间为：（﹣∞，2），（3，+∞）

（2）解：∵对任意x∈[1，4]，函数f（x）的图象恒在函数g（x）=x+4图象的下方，

∴x|x﹣a|+x＜x+4对任意x∈[1，4]，恒成立，

∴x|x﹣a|＜4，∴|x﹣4|＜ ，

∴ ，

即 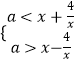对任意x∈[1，4]，恒成立，

令g（x）=x+ ，则g（x）在[1，2]递减，在[2，4]递增，所以g（x）min=g（2）=4，

所以a＜4，

h（x）=x﹣ ，则h（x）在x∈[1，4]，上为增函数，所以h（x）max=h（4）=3，所以a＞3，

∴3＜a＜4

【解析】（1）本小题将含有绝对值的函数去掉绝对值以后变为分段函数，然后求得函数的单调递增区间；（2）将“函数f（x）的图象恒在函数g（x）=x+4图象的下方”转化为含绝对值的不等式问题进行求解.