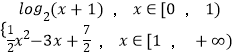题目内容
【题目】在平面直角坐标系xOy中，已知圆C1：x2+y2=16和圆C2：（x﹣7）2+（y﹣4）2=4，
（1）求过点（4，6）的圆C1的切线方程；
（2）设P为坐标平面上的点，且满足：存在过点P的无穷多对互相垂直的直线l1和l2 ， 它们分别与圆C1和圆C2相交，且直线l1被圆C1截得的弦长是直线l2被圆C2截得的弦长的2倍．试求所有满足条件的点P的坐标．
【答案】
（1）解：若切线的斜率存在，可设切线的方程为y﹣6=k（x﹣4），
则圆心C1到切线的距离 
，解得 
，
所以切线的方程为：5x﹣12y+52=0；
若切线的斜率不存在，则切线方程为x=4，符合题意．
综上所述，过P点的圆C1的切线方程为5x﹣12y+52=0或x=4
（2）解：设点P（a，b）满足条件，不妨设直线l1的方程为：y﹣b=k（x﹣a）（k≠0），
即kx﹣y+b﹣ak=0（k≠0），
则直线l2的方程为： 
，即x+ky﹣bk﹣a=0．
因为圆C1的半径是圆C2的半径的2倍，
及直线l1被圆C1截得的弦长是直线l2被圆C2截得的弦长的2倍，
所以圆C1的圆心到直线l1的距离是圆C2的圆心到直线l2的距离的2倍，
即 
整理得|ak﹣b|=|2a﹣14+（2b﹣8）k|
从而ak﹣b=2a﹣14+（2b﹣8）k或b﹣ak=2a﹣14+（2b﹣8）k，
即（a﹣2b+8）k=2a+b﹣14或（a+2b﹣8）k=﹣2a+b+14，
因为k的取值有无穷多个，所以 
或 
，
解得 
或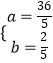 
，这样点P只可能是点P1（4，6）或点 
．
经检验点P1和点P2满足题目条件
【解析】（1）分类讨论，利用圆心到直线的距离等于半径，建立方程，求出k，即可求过点（4，6）的圆C1的切线方程；（2）设出过P点的直线l1与l2的点斜式方程，根据⊙C1和⊙C2的半径，及直线l1被圆C1截得的弦长是直线l2被圆C2截得的弦长的2，可得⊙C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离2倍，故我们可以得到一个关于直线斜率k的方程，即可以求所有满足条件的点P的坐标．
