题目内容
【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．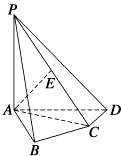 
（1）求PB和平面PAD所成的角的大小；
（2）证明：AE⊥平面PCD；
（3）求二面角A﹣PD﹣C得到正弦值．
【答案】
（1）解：在四棱锥P﹣ABCD中，
∵PA⊥底面ABCD，AB平面ABCD，
∴PA⊥AB，又AB⊥AD，PA∩AD=A，
∴AB⊥平面PAD，∴∠APB是PB与平面PAD所成的角，
在Rt△PAB中，AB=PA，∴∠APB=45°，
∴PB和平面PAD所成的角的大小为45°
（2）解：证明：在四棱锥P﹣ABCD中，
∵PA⊥底面ABCD，CD平面ABCD，∴CD⊥PA，
由条件AC⊥CD，PA⊥底面ABCD，利用三垂线定理得CD⊥PC，PA∩AC=A，
∴CD⊥面PAC，
又AE面PAC，∴AE⊥CD，
由PA=AB=BC，∠ABC=60°，得AC=PA，
∵E是PC的中点，∴AE⊥PC，
又PC∩CD=C，
综上，AE⊥平面PCD
（3）解：过点E作EM⊥PD，AM在平面PCD内的射影是EM，则AM⊥PD，
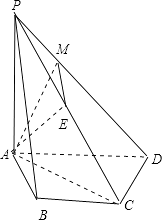
∴∠AME是二面角A﹣PD﹣C的平面角，
由已知得∠CAD=30°，
设AC=a，得PA=a，AD= 
，PD= 
，AE= 
，
在Rt△ADP中，∵AM⊥PD，∴AMPD=PAAD，
∴AM= 
= 
，
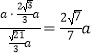在Rt△AEM中，sin∠AME= 
．
∴二面角A﹣PD﹣C得到正弦值为 ．
【解析】（1）由线面垂直得PA⊥PB，又AB⊥AD，从而AB⊥平面PAD，进而∠APB是PB与平面PAD所成的角，由此能求出PB和平面PAD所成的角的大小．（2）由线面垂直得CD⊥PA，由条件CD⊥PC，得CD⊥面PAC，由等腰三角形得AE⊥PC，由此能证明AE⊥平面PCD．（3）过点E作EM⊥PD，AM在平面PCD内的射影是EM，则AM⊥PD，由此得∠AME是二面角A﹣PD﹣C的平面角，由此能求出二面角A﹣PD﹣C得到正弦值．
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想，以及对空间角的异面直线所成的角的理解，了解已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则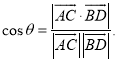
．
