题目内容
请阅读下列材料：若两个正实数a1，a2满足a12＋a22＝1，那么a1＋a2≤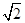
.
证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.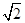
根据上述证明方法，若n个正实数满足a12＋a22＋…＋an2＝1时，你能得到的结论为________．
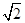.证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤
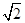.根据上述证明方法，若n个正实数满足a12＋a22＋…＋an2＝1时，你能得到的结论为________．
a1＋a2＋…＋an≤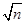
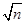
构造函数f(x)＝(x－a1)2＋(x－a2)2＋…＋(x－an)2＝nx2－2(a1＋a2＋…＋an)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，
从而得4(a1＋a2＋…＋an)2－4n≤0，
所以a1＋a2＋…＋an≤.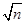
从而得4(a1＋a2＋…＋an)2－4n≤0，
所以a1＋a2＋…＋an≤
.
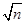练习册系列答案
名校课堂系列答案
相关题目
，试证明
至少有一个不小于1.
都是正实数，且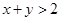
.求证：
与
中至少有一个成立.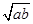
.
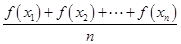≤f(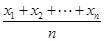
)，已知函数y＝sinx在区间(0，π)上是凸函数，则在△ABC中，sinA＋sinB＋sinC的最大值为________．
＋
，
＋
，
＋
( )
（
是互不相等的实数），三条抛物线至少有一条与
轴有两个交点．