题目内容
设函数f(x)=ex-e-x
(Ⅰ)证明:f(x)的导数f′(x)≥2;
(Ⅱ)若对所有x≥0都有f(x)≥ax,求a的取值范围.
(Ⅰ)证明:f(x)的导数f′(x)≥2;
(Ⅱ)若对所有x≥0都有f(x)≥ax,求a的取值范围.
(Ⅰ)f(x)的导数f'(x)=ex+e-x.
由于ex+e-x≥2
=2,故f'(x)≥2.
(当且仅当x=0时,等号成立).
(Ⅱ)令g(x)=f(x)-ax,则g'(x)=f'(x)-a=ex+e-x-a,
(ⅰ)若a≤2,当x>0时,g'(x)=ex+e-x-a>2-a≥0,
故g(x)在(0,+∞)上为增函数,
所以,x≥0时,g(x)≥g(0),即f(x)≥ax.
(ⅱ)若a>2,方程g'(x)=0的正根为x1=ln
,
此时,若x∈(0,x1),则g'(x)<0,故g(x)在该区间为减函数.
所以,x∈(0,x1)时,g(x)<g(0)=0,即f(x)<ax,与题设f(x)≥ax相矛盾.
综上,满足条件的a的取值范围是(-∞,2].
由于ex+e-x≥2
| ex•e-x |
(当且仅当x=0时,等号成立).
(Ⅱ)令g(x)=f(x)-ax,则g'(x)=f'(x)-a=ex+e-x-a,
(ⅰ)若a≤2,当x>0时,g'(x)=ex+e-x-a>2-a≥0,
故g(x)在(0,+∞)上为增函数,
所以,x≥0时,g(x)≥g(0),即f(x)≥ax.
(ⅱ)若a>2,方程g'(x)=0的正根为x1=ln
a+
| ||
| 2 |
此时,若x∈(0,x1),则g'(x)<0,故g(x)在该区间为减函数.
所以,x∈(0,x1)时,g(x)<g(0)=0,即f(x)<ax,与题设f(x)≥ax相矛盾.
综上,满足条件的a的取值范围是(-∞,2].

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 圆
圆 与
与 轴正半轴的交点为
轴正半轴的交点为 ,与曲线
,与曲线 的交点为
的交点为 ,直线
,直线 与
与 轴的交点为
轴的交点为 .
. 表示
表示 和
和
 满足
满足
 的值,使得数列
的值,使得数列 成等比数列;
成等比数列; 的大小.
的大小.
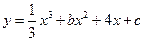 (c为实常数)上任意一点为切点的切线的斜率恒为非负数,则实数b的取值范围为 。
(c为实常数)上任意一点为切点的切线的斜率恒为非负数,则实数b的取值范围为 。