题目内容
16.下列五个命题:①“a>2”是“f(x)=ax-sinx为R上的增函数”的充分不必要条件;
②函数f(x)=-$\frac{1}{3}{x^3}$+x+1有两个零点;
③集合A={2,3},B={1,2,3},从A,B中各任意取一个数,则这两数之和等于4的概率是$\frac{1}{3}$;
④动圆C既与定圆(x-2)2+y2=4相外切,又与y轴相切,则圆心C的轨迹方程是y2=8x(x≠0);
⑤若函数f(x)=aln(x+2)+$\frac{x}{{{x^2}+1}}$(x>-2,a∈R)有最大值,则f(x)一定有最小值.其中正确的命题序号是①③⑤.
分析 利用导数法求出f(x)=ax-sinx为R上的增函数等价命题,进而根据充要条件的定义,可判断①;
求出函数$f(x)=-\frac{1}{3}{x^3}+x+1$的零点个数,可判断②;
求出从A,B中各任意取一个数,则这两数之和等于4的概率,可判断③;
求出圆心C的轨迹方程,可判断④;
根据函数有最大值,求出a值,进而判断函数最小值是否存在,可判断⑤.
解答 解:当f(x)=ax-sinx时,f′(x)=a-cosx,当a≥1时,f′(x)≥0在R上恒成立,f(x)=ax-sinx为R上的增函数,
由{a|a>2}?{a|a≥1},故“a>2”是“f(x)=ax-sinx为R上的增函数”的充分不必要条件,即①正确;
当函数$f(x)=-\frac{1}{3}{x^3}+x+1$时,f′(x)=-x2+1,令f′(x)=0,则x=±1,根据三次函数的图象和性质,可得当x=-1时,f(x)的极小值$\frac{1}{3}$>0,故f(x)仅有一个零点,故②错误;
集合A={2,3},B={1,2,3},从A,B中各任意取一个数共有2×3=6种情况,其中这两数之和等于4有(2,2),(3,1)两种情况,故这两数之和等于4的概率是$\frac{2}{6}$=$\frac{1}{3}$,故③正确;
动圆C既与定圆(x-2)2+y2=4相外切,又与y轴相切,则圆心C的轨迹方程是y2=8x(x≠0)或y=0(x<0),故④错误;
如果a>0,则$\underset{lim}{x→+∞}$f(x)=+∞,则f(x)无最大值;如果a<0,则$\underset{lim}{x→-2}$f(x)=+∞,则f(x)无最大值;故a=0,
即f(x)=$\frac{x}{{{x^2}+1}}$(x>-2,a∈R),当x=-1时,函数取最小值-$\frac{1}{2}$,故⑤正确;
故正确的命题序号是①③⑤;
故答案为:①③⑤
点评 本题以命题的真假判断为载体,考查了充要条件,函数的单调性,函数的零点,概率,直线与圆的位置关系,圆与圆的位置关系,轨迹方程,恒成立问题等知识点,综合性强,属于中档题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | 分别表示空间向量的有向线段所在直线是异面直线,则这两个向量不是共面向量 | |
| B. | 若$|{\overrightarrow a}|=|{\overrightarrow b}|$,则$\overrightarrow a,\overrightarrow b$的长度相等而方向相同或相反 | |
| C. | 若向量$\overrightarrow{AB},\overrightarrow{CD}$满足$|{\overrightarrow{AB}}|>|{\overrightarrow{CD}}|$,且$\overrightarrow{AB}与\overrightarrow{CD}$同向,则$\overrightarrow{AB}>\overrightarrow{CD}$ | |
| D. | 若两个非零向量$\overrightarrow{AB},\overrightarrow{CD}$满足$\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow 0$,则$\overrightarrow{AB}$∥$\overrightarrow{CD}$ |
| A. | 24 | B. | 32 | C. | 36 | D. | 72 |
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| B. | 若A,B,C,D是不共线的四点,则$\overrightarrow{AB}$=$\overrightarrow{DC}$是四边形ABCD是平行四边形的等价条件 | |
| C. | 若非零向量$\overrightarrow{AB}$∥$\overrightarrow{CD}$,那么AB∥CD | |
| D. | $\overrightarrow{AB}$=$\overrightarrow{CD}$的等价条件是A与C重合,B与D重合 |
 已知正方形ABCD,HG⊥平面ABCD,G,F分别为AB,BC的中点,E为AC上一点,且AE=3EC,求证:EF为异面直线AC与HF的公垂线.
已知正方形ABCD,HG⊥平面ABCD,G,F分别为AB,BC的中点,E为AC上一点,且AE=3EC,求证:EF为异面直线AC与HF的公垂线.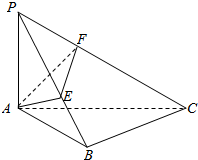 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证: