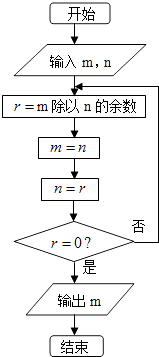
题目内容
【题目】已知 圆![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() ,且
,且![]() (
(![]() 为原点).
为原点).
(![]() )求点
)求点![]() 的轨迹方程.
的轨迹方程.
(![]() )求四边形
)求四边形![]() 面积的最小值.
面积的最小值.
(![]() )设
)设![]() ,
, ![]() ,在圆
,在圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求
,求![]() 的最大值和最小值(直接写出结果即可).
的最大值和最小值(直接写出结果即可).
【答案】(1) 点![]() 轨迹方程为
轨迹方程为![]() ;(2)
;(2) 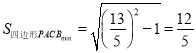 ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)根据题意得到:设![]() 为
为![]() ,由勾股定理得到
,由勾股定理得到![]() ,根据点点距得到轨迹方程;(2)
,根据点点距得到轨迹方程;(2)![]() ,转化为动点到定点的距离;(3)因为
,转化为动点到定点的距离;(3)因为![]() ,故点
,故点![]() 是以
是以![]() 为直径的圆
为直径的圆![]() 与圆
与圆![]() 的交点,当圆
的交点,当圆![]() 与圆
与圆![]() 内切时,圆
内切时,圆![]() 直径
直径![]() 最大,外切时有最小值.
最大,外切时有最小值.
解析:
(![]() )∵
)∵![]() ,
,
∴![]() ,
,
又![]() 是圆
是圆![]() 切线,
切线,
∴![]() .
.
设![]() 为
为![]() ,
,
∵![]() ,
,
∴![]() ,
,
化简得![]() ,
,
故点![]() 轨迹方程为
轨迹方程为![]() .
.
(![]() )
)![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
当![]() 最小时,
最小时,
即点![]() 到
到![]() 所在直线方程的距离,
所在直线方程的距离,
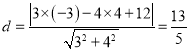 ,
,
![]() .
.
∴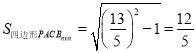 .
.
(![]() )∵
)∵![]() ,∴点
,∴点![]() 是以
是以![]() 为直径的圆
为直径的圆![]() 与圆
与圆![]() 的交点,∴当圆
的交点,∴当圆![]() 与圆
与圆![]() 内切时,
内切时,
圆![]() 直径
直径![]() 最大,此时
最大,此时![]() ,∴
,∴![]() ,
,
当圆![]() 与圆
与圆![]() 外切时,圆
外切时,圆![]() 直径
直径![]() 最小,此时
最小,此时![]() ,
,
∴![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目