题目内容
9. 某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为$2\sqrt{2}$.
某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为$2\sqrt{2}$.
分析 由主视图知CD⊥平面ABC、B点在AC上的射影为AC中点及AC长,由左视图可知CD长及△ABC中变AC的高,利用勾股定理即可求出最长棱BD的长.
解答 解:由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=1;
由主视图知CD=2,由左视图知BE=1,
在Rt△BCE中,BC=$\sqrt{2}$,
在Rt△BCD中,BD=$\sqrt{6}$,
在Rt△ACD中,AD=2$\sqrt{2}$.
则三棱锥中最长棱的长为2$\sqrt{2}$.
故答案为:$2\sqrt{2}$
点评 本题考查点、线、面间的距离计算,考查空间图形的三视图,考查学生的空间想象能力,考查学生分析解决问题的能力.

练习册系列答案
相关题目
20.如图是一个几何体的三视图,其俯视图的面积为8$\sqrt{2}$,则该几何体的表面积为( )


| A. | 8 | B. | 20+8$\sqrt{2}$ | C. | 16 | D. | 24+8$\sqrt{2}$ |
17.已知复数z=5+6i,则|z+$\overline{z}$|的值为( )
| A. | 12 | B. | 12i | C. | -10 | D. | 10 |
4.若$\frac{cos(2α-π)}{sin(α+\frac{π}{4})}$=$\frac{\sqrt{2}}{2}$,则sinα-cosα的值为( )
| A. | -$\frac{\sqrt{7}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
19.设1,a+bi,b+ai是一等比数列的连续三项,则a,b的值分别为( )
| A. | a=±$\frac{\sqrt{3}}{2}$,b=±$\frac{1}{2}$ | B. | a=-$\frac{1}{2}$,b=$\frac{\sqrt{3}}{2}$ | C. | a=±$\frac{\sqrt{3}}{2}$,b=$\frac{1}{2}$ | D. | a=-$\frac{1}{2}$,b=-$\frac{\sqrt{3}}{2}$ |
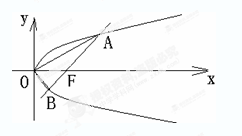 过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.