题目内容
【题目】已知函数![]() ,若同时满足以下条件:
,若同时满足以下条件:
①![]() 在D上单调递减或单调递增;
在D上单调递减或单调递增;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么称
,那么称![]() 为闭函数.
为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是不是闭函数?若是请找出区间
是不是闭函数?若是请找出区间![]() ;若不是请说明理由;
;若不是请说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)由![]() 在R上单减,列出方程组,即可求
在R上单减,列出方程组,即可求![]() 的值;
的值;
(2)由函数y=2x+lgx在(0,+∞)单调递增可知![]() 即
即![]() ,结合对数函数的单调性可判断
,结合对数函数的单调性可判断
(3)易知![]() 在[﹣2,+∞)上单调递增.设满足条件B的区间为[a,b],则方程组
在[﹣2,+∞)上单调递增.设满足条件B的区间为[a,b],则方程组![]() 有解,方程
有解,方程![]() 至少有两个不同的解,即方程x2﹣(2k+1)x+k2﹣2=0有两个都不小于k的不根.结合二次方程的实根分布可求k的范围
至少有两个不同的解,即方程x2﹣(2k+1)x+k2﹣2=0有两个都不小于k的不根.结合二次方程的实根分布可求k的范围
解:(1)∵![]() 在R上单减,所以区间[a,b]满足
在R上单减,所以区间[a,b]满足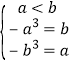 ,
,
解得a=﹣1,b=1
(2)∵函数y=2x+lgx在(0,+∞)单调递增
假设存在满足条件的区间[a,b],a<b,则![]() ,即
,即![]()
∴lgx=﹣x在(0,+∞)有两个不同的实数根,但是结合对数函数的单调性可知,y=lgx与y=﹣x只有一个交点
故不存在满足条件的区间[a,b],函数y=2x+lgx是不是闭函数
(3)易知![]() 在[﹣2,+∞)上单调递增.
在[﹣2,+∞)上单调递增.
设满足条件B的区间为[a,b],则方程组![]() 有解,方程
有解,方程![]() 至少有两个不同的解
至少有两个不同的解
即方程x2﹣(2k+1)x+k2﹣2=0有两个都不小于k的不根.
∴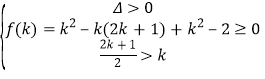 得
得![]() ,即所求.
,即所求.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目



