题目内容
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
(1)求证:A1C⊥平面BDE;
(2)求A1B与平面BDE所成角的正弦值。
(3)设F是CC1上的动点(不包括端点C),求证:△DBF是锐角三角形。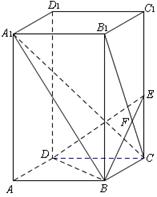
(1)求证:A1C⊥平面BDE;
(2)求A1B与平面BDE所成角的正弦值。
(3)设F是CC1上的动点(不包括端点C),求证:△DBF是锐角三角形。

(1)见解析
(2)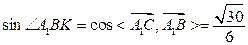
(3)见解析
(2)
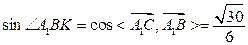
(3)见解析
(1)证明:由正四棱柱性质知A1B1⊥平面BCC1B1,A1A⊥平面ABCD,
所以B1C、AC分别是A1C在平面CC1B1B、平面ABCD上的射影
∵ B1C⊥BE, AC⊥BD, ∴A1C⊥BE , A1C⊥BD, (2分)
∴ A1C⊥平面BDE (4分)。 (直接指出根据三垂线定理得“A1C⊥BE , A1C⊥BD”而推出结论的不扣分)
(2)解:以DA、DC、DD1所在直线分别为x、y、z轴,建立坐标系,则
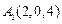 ,
,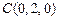 ,
,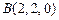 ,∴
,∴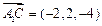 ,
,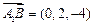 (6分)
(6分)∴
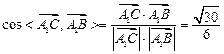 (7分)
(7分)设A1C
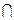 平面BDE=K,
平面BDE=K,由(1)可知,∠A1BK为A1B与平面BDE所成角,(8分)
∴
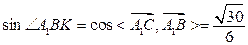 (9分)
(9分)(3)证明:设点F的坐标为(0, 2, z)(0<z≤4), 则
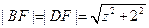 ,
,又|DB|=
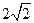 ,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。 (11分)
,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。 (11分)由余弦定理得cos∠DFB=
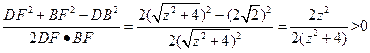
∴∠DFB为锐角, (13分)
即不论点F为CC1上C点除外的任意一点, △DFB总是锐角三角形.(14分)
说明: 若没有说明三角形为等腰三角形而只证明一个角是锐角,或只证明底角是锐角的“以偏概全”情况应扣2分)

练习册系列答案
相关题目
 平面
平面 ,
,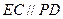 ,且
,且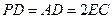 ="2" .
="2" .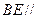 平面
平面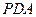 .
.
 平面CDE,且
平面CDE,且 ,
, .
. 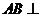 平面
平面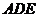 ;
;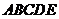 的体积.
的体积.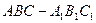 中,
中,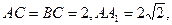 ∠ACB=90°,M是
∠ACB=90°,M是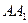 的中点,N是
的中点,N是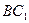 的中点。
的中点。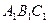 ;
;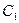 到平面BMC的距离;
到平面BMC的距离;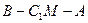 1的大小。
1的大小。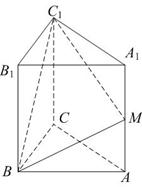
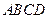 中,
中,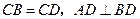 ,点
,点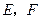 分别是
分别是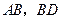 的中点.
的中点.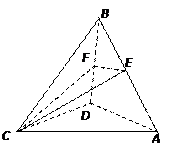
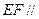 面
面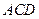 ;
;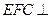 面
面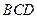 .
.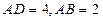 ,E、F分别是线段AB、BC的中点,
,E、F分别是线段AB、BC的中点,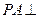 面ABCD. (1)
面ABCD. (1)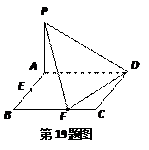 证明:PF⊥FD;
证明:PF⊥FD; ,其
,其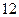 条棱的长度之和为
条棱的长度之和为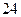 ,则这个长方体的一条
,则这个长方体的一条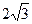
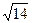
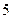
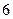
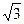 ,BC=CD=3,AC=
,BC=CD=3,AC=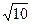 ,BD=2.
,BD=2.