题目内容
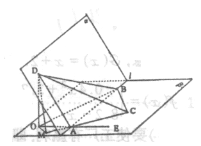
在四面体ABCD中,AB=AD=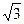 ,BC=CD=3,AC=
,BC=CD=3,AC=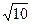 ,BD=2.
,BD=2.
(1)平面ABD与平面BCD是否垂直?证明你的结论;(2)求二面角A-CD-B的正切值。
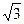 ,BC=CD=3,AC=
,BC=CD=3,AC=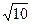 ,BD=2.
,BD=2.(1)平面ABD与平面BCD是否垂直?证明你的结论;(2)求二面角A-CD-B的正切值。
(1)垂直;(2)二面角A-CD-B的正切值为 。
。
 。
。如图,(1)垂直。证明如下:设BD的中点为E,连AE,CE。
∵AB=AD∴AE⊥BD。同理CE⊥BD。
∴AE= ,
,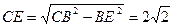
∵AC=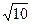 ,∴AC2=AE2+CE2∴∠AEC=90°即AE⊥EC
,∴AC2=AE2+CE2∴∠AEC=90°即AE⊥EC
∴AE⊥平面BCD∵AE 平面ABD∴平面ABD⊥平面BCD
平面ABD∴平面ABD⊥平面BCD
(2)作EF⊥CD于F,连结AF。∵AE⊥平面BCD∴AF⊥CD
∴∠AFE就是二面角A-CD-B的平面角,
∴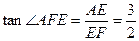 即二面角A-CD-B的正切值为
即二面角A-CD-B的正切值为 。
。

∵AB=AD∴AE⊥BD。同理CE⊥BD。
∴AE=
 ,
,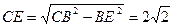
∵AC=
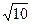 ,∴AC2=AE2+CE2∴∠AEC=90°即AE⊥EC
,∴AC2=AE2+CE2∴∠AEC=90°即AE⊥EC∴AE⊥平面BCD∵AE
 平面ABD∴平面ABD⊥平面BCD
平面ABD∴平面ABD⊥平面BCD(2)作EF⊥CD于F,连结AF。∵AE⊥平面BCD∴AF⊥CD
∴∠AFE就是二面角A-CD-B的平面角,

∴
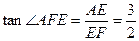 即二面角A-CD-B的正切值为
即二面角A-CD-B的正切值为 。
。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
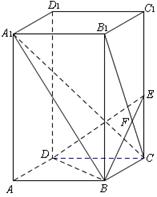
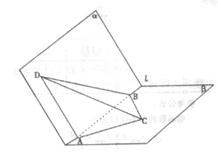
 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。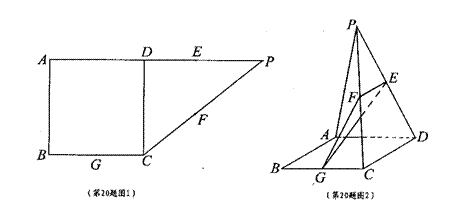
 平面PEG
平面PEG
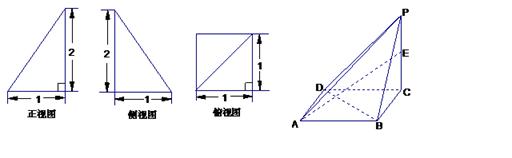

 中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA
中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA ="2, " E、E
="2, " E、E ∥平面
∥平面 ;
; 

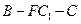 的余弦值
的余弦值
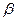 是120°的二面角,A,B两点在棱上,AB=2,D在
是120°的二面角,A,B两点在棱上,AB=2,D在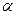 内,三角形ABD是等腰直角三角形,∠DAB=90°,C在
内,三角形ABD是等腰直角三角形,∠DAB=90°,C在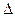 ABC是等腰直角三角形∠ACB=
ABC是等腰直角三角形∠ACB=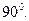
 中,底面
中,底面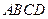 是矩形,
是矩形,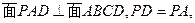
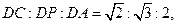
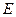 是
是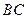 的中点,
的中点,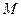 是
是 的中点。
的中点。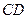 与
与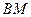 所成的角;(Ⅱ)求二面角
所成的角;(Ⅱ)求二面角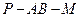 的大小。
的大小。