题目内容
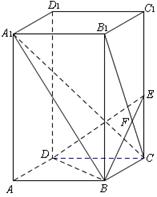
(本小题满分12分)已知ABCD是矩形,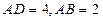 ,E、F分别是线段AB、BC的中点,
,E、F分别是线段AB、BC的中点,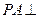 面ABCD. (1)
面ABCD. (1)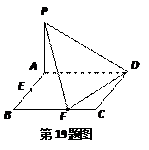 证明:PF⊥FD;
证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD.
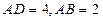 ,E、F分别是线段AB、BC的中点,
,E、F分别是线段AB、BC的中点, 面ABCD. (1)
面ABCD. (1) 证明:PF⊥FD;
证明:PF⊥FD;(2)在PA上找一点G,使得EG∥平面PFD.
(Ⅰ) 见解析 (Ⅱ) 

(1) 证明:连结AF,
∵在矩形ABCD中,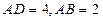 ,F是线段BC的中点,∴AF⊥FD.
,F是线段BC的中点,∴AF⊥FD.
又∵PA⊥面ABCD,∴PA⊥FD. ∴平面PAF⊥FD. ∴PF⊥FD. ……5分
(2) 过E作EH∥FD交AD于H,则EH∥平面PFD且 .
.
再过H作HG∥DP交PA于G,则HG∥平面PFD且 .
.
∴平面EHG∥平面PFD. ∴EG∥平面PFD.从而满足 的点G为所找.……12分
的点G为所找.……12分
∵在矩形ABCD中,
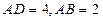 ,F是线段BC的中点,∴AF⊥FD.
,F是线段BC的中点,∴AF⊥FD.又∵PA⊥面ABCD,∴PA⊥FD. ∴平面PAF⊥FD. ∴PF⊥FD. ……5分
(2) 过E作EH∥FD交AD于H,则EH∥平面PFD且
 .
.再过H作HG∥DP交PA于G,则HG∥平面PFD且
 .
.∴平面EHG∥平面PFD. ∴EG∥平面PFD.从而满足
 的点G为所找.……12分
的点G为所找.……12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


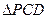 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。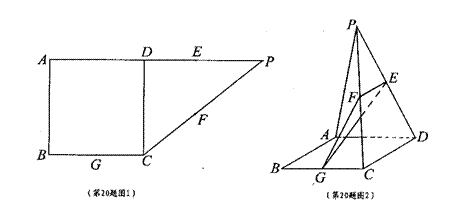
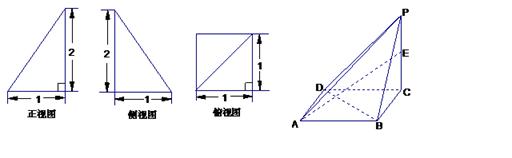
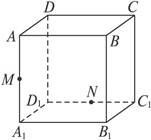
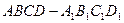 的棱长为2
的棱长为2 ,E为AB的中点.(Ⅰ)求证:
,E为AB的中点.(Ⅰ)求证: (Ⅱ)求异面直线BD1与CE所成角的余弦值;(Ⅲ)求点B到平面
(Ⅱ)求异面直线BD1与CE所成角的余弦值;(Ⅲ)求点B到平面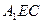 的距离.
的距离.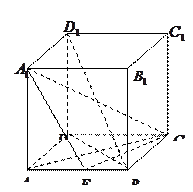
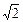 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
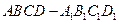 中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA
中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA ="2, " E、E
="2, " E、E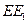 ∥平面
∥平面 ;
; 

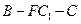 的余弦值
的余弦值