题目内容
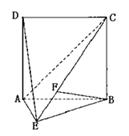
如图,平面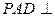 平面ABCD,ABCD为正方形,
平面ABCD,ABCD为正方形,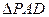 是直角三角形,且
是直角三角形,且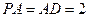 ,E、F、G分别是线段PA,PD,CD的中点.
,E、F、G分别是线段PA,PD,CD的中点.
(1)求证: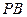 ∥面EFC;
∥面EFC;
(2)求异面直线EG与BD所成的角;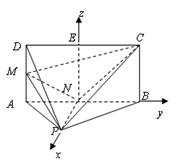
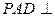 平面ABCD,ABCD为正方形,
平面ABCD,ABCD为正方形,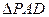 是直角三角形,且
是直角三角形,且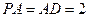 ,E、F、G分别是线段PA,PD,CD的中点.
,E、F、G分别是线段PA,PD,CD的中点.(1)求证:
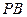 ∥面EFC;
∥面EFC;(2)求异面直线EG与BD所成的角;

(1)证明见解析(2)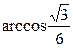
(1)证明:取AB中点H,连结GH,HE,∵E,F,G分别是线段PA、PD、CD的中点,∴GH∥AD∥EF,∴E,F,G,H四点共面,又H为AB中点,∴EH∥PB.又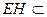 面EFG,PB
面EFG,PB 面EFG,∴PB∥面EFG.………6分
面EFG,∴PB∥面EFG.………6分
(2)取BC的中点M,连结GM、AM、EM,则GM∥BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.
在Rt△MAE中,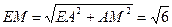 ,同理
,同理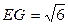 ,
,
又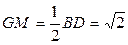 ,∴在MGE中,
,∴在MGE中,
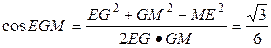 ,
,
故异面直线EG与BD所成的角为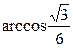 .………………12分
.………………12分
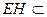 面EFG,PB
面EFG,PB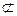 面EFG,∴PB∥面EFG.………6分
面EFG,∴PB∥面EFG.………6分(2)取BC的中点M,连结GM、AM、EM,则GM∥BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.
在Rt△MAE中,
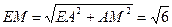 ,同理
,同理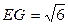 ,
,又
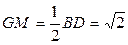 ,∴在MGE中,
,∴在MGE中,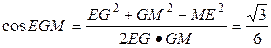 ,
,故异面直线EG与BD所成的角为
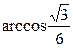 .………………12分
.………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
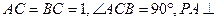 平面ABC,CE//PA,PA=2CE=2。
平面ABC,CE//PA,PA=2CE=2。 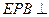 平面APB; (2)求二面角A—BE—P的正弦值。
平面APB; (2)求二面角A—BE—P的正弦值。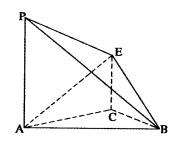
 中,底面
中,底面 为正方形,且
为正方形,且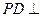 平面
平面 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.
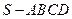 中,底面
中,底面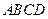 是正方形,
是正方形,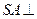 底面
底面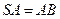 , 点
, 点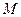 是
是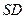 的中点,
的中点,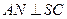 ,且交
,且交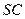 于点
于点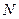 .
.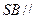 平面
平面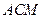 ;
;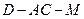 的余弦值大小;
的余弦值大小;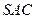 ⊥平面
⊥平面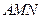 .
.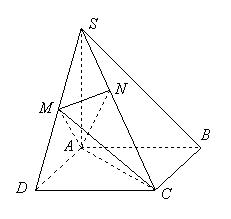
 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,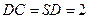 ,点
,点 在侧棱
在侧棱 上,
上,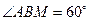 。
。
 的大小。
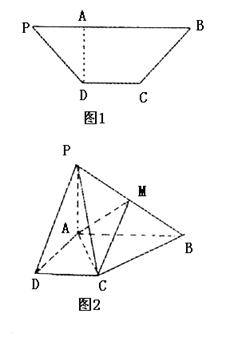
的大小。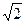 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面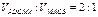 ;
;
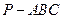 中,⊿
中,⊿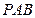 是等边三角形,∠PAC=∠PBC="90" º.
是等边三角形,∠PAC=∠PBC="90" º.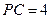 ,且平面
,且平面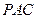 ⊥平面
⊥平面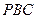 ,求三棱锥
,求三棱锥
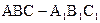 与正三棱锥
与正三棱锥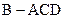 组成,其中,
组成,其中, .它的正视图、俯视图、从左向右的侧视图的面积分别为
.它的正视图、俯视图、从左向右的侧视图的面积分别为 ,
, .
.
 与平面
与平面 所成角的正弦;
所成角的正弦;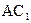 上是否存在点
上是否存在点 ,使
,使 平面
平面