题目内容
20.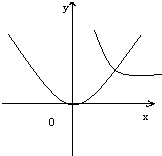 已知曲线y=$\frac{1}{x}$和y=x2它们交于点P,过P点的两条切线与x轴分别交于A,B两点.求△ABP的面积.
已知曲线y=$\frac{1}{x}$和y=x2它们交于点P,过P点的两条切线与x轴分别交于A,B两点.求△ABP的面积.
分析 联立两曲线方程求出交点坐标P(1,1),把x=1分别代入两曲线的导函数中求两切线的斜率,从而写出过点P的两条切线方程,然后根据与x轴交点坐标的求法分别求出A、B的坐标可确定出三角形的底与高,利用三角形的面积公式即可求出.
解答 解:联立两曲线方程得$\left\{\begin{array}{l}y=\frac{1}{x}\\ y={x}^{2}\end{array}\right.$,
解得$\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$,
所以切点P的坐标为(1,1),
求出两曲线的导函数为y′=-$\frac{1}{{x}^{2}}$和y′=2x,把x=1分别代入两个导函数得到过p点切线的斜率分别为:k1=-1,k2=2×1=2,
则两曲线在P点的切线方程分别为:y-1=-1(x-1)即x+y-2=0;y-1=2(x-1)即2x-y-1=0
因为A、B是两切线与x轴的交点,所以令y=0,得到A(2,0),B($\frac{1}{2}$,0),
则s△ABP=$\frac{1}{2}$×|2-$\frac{1}{2}$|×1=$\frac{3}{4}$.
点评 此题是把函数与方程综合在一起的题型,要求学生会利用导数求切线的斜率,以及会根据一点和斜率写出直线的方程,会求直线与x轴的截距.

练习册系列答案
相关题目
15.函数y=3x的反函数是( )
| A. | y=x3 | B. | y=$\root{3}{x}$ | C. | y=log3x | D. | y=($\frac{1}{3}$)x |
5.若复数z满足$\frac{z}{1+2i}$=|3-4i|,则z的共轭复数$\overline{z}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.在区间(-1,1)内任取两个实数,则这两个实数的绝对值之和小于1的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
10.四边形OABC中,$\overrightarrow{CB}=\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OA}=\overrightarrow a$,$\overrightarrow{OC}=\overrightarrow b$,则$\overrightarrow{AB}$=( )
| A. | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ | B. | $\frac{\overrightarrow a}{2}-\overrightarrow b$ | C. | $\overrightarrow b+\frac{\overrightarrow a}{2}$ | D. | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ |