题目内容
【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F. 
(1)证明:C,E,F,D四点共圆;
(2)若D为BC的中点,且AF=3,FD=1,求AE的长.
【答案】
(1)证明:连结EF,BE,则∠ABE=∠AFE,因为AB是⊙O是直径,
所以,AE⊥BE,又因为AB⊥BC,∠ABE=∠C,
所以∠AFE=∠C,即∠EFD+∠C=180°,
∴C,E,F,D四点共圆.
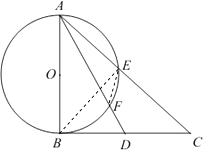
(2)解:因为AB⊥BC,AB是直径,
所以,BC是圆的切线,DB2=DFDA=4,即BD=2,
所以,AB= ![]() =2
=2 ![]() ,
,
因为D为BC的中点,所以BC=4,AC= ![]() =2
=2 ![]() ,
,
因为C、E、F、D四点共圆,所以AEAC=AFAD,
即2 ![]() AE=12,即AE=
AE=12,即AE= ![]()
【解析】(1)连结EF,BE,说明AB是⊙O是直径,推出∠ABE=∠C,然后证明C,E,F,D四点共圆.(2)利用切割线定理求解BD,利用C、E、F、D四点共圆,得到AEAC=AFAD,然后求解AE.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目