题目内容
已知正方体ABCD-A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1、CC1的中点,求证:平面EB1D1∥平面FBD.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1、CC1的中点,求证:平面EB1D1∥平面FBD.
证明:(1)由B1B∥DD1,且B1B=DD1,得B1D1∥BD.
因为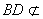
平面B1D1C,
而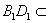
平面B1D1C,
所以BD∥平面B1D1C.
同理A1D∥平面B1D1C.
又A1D∩BD=D,所以平面A1BD∥平面B1D1C.
(2)由BD∥B1D1,得BD∥平面EB1D1.
取BB1中点G,连结AG、GF,
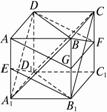
则AE∥B1G且AE=B1G,
所以B1E∥AG.
由GF∥BC且GF=BC,BC∥AD,
得GF∥AD且GF=AD,
所以AG∥DF且AG=DF.
所以B1E∥DF.
所以DF∥平面EB1D1.
所以平面EB1D1∥平面FBD.
因为
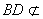平面B1D1C,而
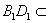平面B1D1C,所以BD∥平面B1D1C.
同理A1D∥平面B1D1C.
又A1D∩BD=D,所以平面A1BD∥平面B1D1C.
(2)由BD∥B1D1,得BD∥平面EB1D1.
取BB1中点G,连结AG、GF,
则AE∥B1G且AE=B1G,
所以B1E∥AG.
由GF∥BC且GF=BC,BC∥AD,
得GF∥AD且GF=AD,
所以AG∥DF且AG=DF.
所以B1E∥DF.
所以DF∥平面EB1D1.
所以平面EB1D1∥平面FBD.
空间直线和平面
练习册系列答案
相关题目
、
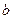成
角，它们的公垂线段为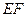
且
，线段AB的长为4，两端点A、B分别在
中，已知
，求异面直线
与
所成角的余弦值 。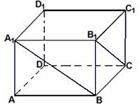
平面
，
，
，
，
，
的大小．
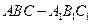中，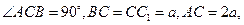
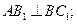（2）求二面角
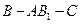的大小；
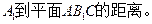
，b与a所成角的余弦为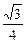
，则b与平面
