��Ŀ����
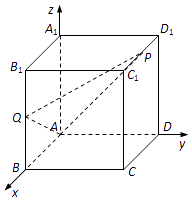
����Ŀ�������غ�ij�γ�ǿ̨���������������ָ����������ӹ���ʦ��ÿ�춼��æµ��һ����������һ�����⣺��ͼ��ʾ����һ�����θְ壬�뾶Ϊ![]() �ף�Բ�Ľ�
�ף�Բ�Ľ�![]() ��ʩ��Ҫ��ͼ���������������ڸְ�
��ʩ��Ҫ��ͼ���������������ڸְ�![]() �ϲ���һ��ƽ���ı��θְ�
�ϲ���һ��ƽ���ı��θְ�![]() ��Ҫ��ʹ���µĸְ����������������ʦ����������⣮����
��Ҫ��ʹ���µĸְ����������������ʦ����������⣮����![]() ����
����![]() ����
����![]() ��
��![]() ������Ϊ
������Ϊ![]() .
.

��1�����߶�![]() �ij��ȣ���
�ij��ȣ���![]() ����ʾ����
����ʾ����
��2����ƽ���ı���![]() ����ı���ʽ����
����ı���ʽ����![]() ����ʾ����
����ʾ����
��3��Ϊʹƽ���ı���![]() ������
������![]() ���ں�ֵ���������Ƕ��٣�
���ں�ֵ���������Ƕ��٣�
���𰸡���1��![]() ��2��
��2��![]() ��3����
��3����![]() ʱ�����øְ��������������Ϊ
ʱ�����øְ��������������Ϊ![]() ƽ���ף�
ƽ���ף�
��������
��1���ȸ���������![]() �б�ʾ
�б�ʾ![]() ������
������![]() �б�ʾ
�б�ʾ![]() ����.
����.
��2���ɣ�1��֪![]() ��
��![]() �� ��
�� ��![]() ��֪
��֪![]() ����ʾƽ���ı������
����ʾƽ���ı������![]() ����϶����ǹ�ʽ���������Ǻ͵����ҹ�ʽ��ʾ����.
����϶����ǹ�ʽ���������Ǻ͵����ҹ�ʽ��ʾ����.
��3���ɣ�2�����![]() �����������ֵ����.
�����������ֵ����.
�⣺��1����![]() �У�
��![]() ��
��![]() ��
��
![]() �ı���
�ı���![]() Ϊƽ���ı���
Ϊƽ���ı���![]() ��
��![]() ��
��![]()
��![]() ��
��![]()
����![]() ��
��
��2��![]() ��
��
��ƽ���ı���![]() �����Ϊ
�����Ϊ![]() ��
��
��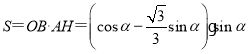
��![]()
��![]()
��![]()
��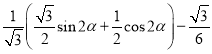
��![]() ��
��
��3������![]() ��
��
����![]() ��
��
��![]() ����
����![]() ʱ��
ʱ��
![]() ��
��
���Ե�![]() ʱ�����øְ��������������Ϊ
ʱ�����øְ��������������Ϊ![]() ƽ���ף�
ƽ���ף�

����Ŀ��Ϊ�˲μ�ij�˶���,����֧��ǿ���������ѡ��18�����Ů��������Ҷ�,��Ա��Դ�������±�:
�ӱ� | ���� | �Ϻ� | ��� | ��һ |
���� | 4 | 6 | 3 | 5 |
(1)����18����Ա�����ѡ������,����������ͬһ�ӵĸ���;
(2)��Ҫ��ѡ��������Ա���������ӳ�,���������Ա����ӵ�����Ϊ![]() ,���������
,���������![]() �ķֲ���.
�ķֲ���.
����Ŀ�����ݹ��һ����������ġ������������������涨��������PM2.5����ƽ��Ũ�Ȳ��ó���35��/�����ף�PM2.5��24Сʱƽ��Ũ�Ȳ��ó���75��/�����ף����л����������ȡ��һ������2016��20��PM2.5��24Сʱƽ��Ũ�ȣ���λ����/�����ף��ļ�����ݣ�����ͳ�������
��� | PM2.5Ũ�� | Ƶ�����죩 | Ƶ�� |
��һ�� | ��0��25] | 3 | 0.15 |
�ڶ��� | ��25��50] | 12 | 0.6 |
������ | ��50��75] | 3 | 0.15 |
������ | ��75��100] | 2 | 0.1 |
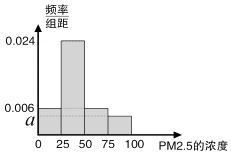
��1������20��IJ���������ϱ��з��鷽�����Ƴɵ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ�� ����ͼ4��a��ֵ��
��������ƽ�������������������������˼�룬��PM2.5����ƽ��Ũ�ȿ��ǣ��жϸþ������Ļ��������Ƿ���Ҫ���ƣ���˵�����ɣ�
��2����Ƶ����Ϊ���ʣ�����2016���ij3�죬����3���иþ�����PM2.5��24Сʱƽ��Ũ�ȷ��ϻ�������������������ΪX����X�ķֲ��к���ѧ������