题目内容
【题目】如图所示,球![]() 的表面积为
的表面积为![]() ,球心
,球心![]() 为空间直角坐标系
为空间直角坐标系![]() 的原点,且球
的原点,且球![]() 分别与
分别与![]() 轴的正交半轴交于
轴的正交半轴交于![]() 三点,已知球面上一点
三点,已知球面上一点![]() .
.
(1)求![]() 两点在球
两点在球![]() 上的球面距离;
上的球面距离;
(2)过点![]() 作平面
作平面![]() 的垂线,垂足
的垂线,垂足![]() ,求
,求![]() 的坐标,并计算四面体
的坐标,并计算四面体![]() 的体积;
的体积;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的大小.
所成锐二面角的大小.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)根据题意求出![]() ,即可得到
,即可得到![]() 两点在球
两点在球![]() 上的球面距离;
上的球面距离;
(2)根据题意,可证![]() 与
与![]() 重合,利用向量可求
重合,利用向量可求![]() ,求出
,求出![]() 的面积,即可得到四面体
的面积,即可得到四面体![]() 的体积;
的体积;
(3)利用空间向量可求面![]() 与平面
与平面![]() 所成锐二面角的大小..
所成锐二面角的大小..
详解:
(1)![]() ,
,
![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
![]() 两点在球
两点在球![]() 上的球面距离
上的球面距离![]() ;
;
(2)![]() ,
,
![]() 面
面![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴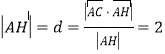 ,
,
∴![]() 与
与![]() 重合,
重合,
∴![]() ,
,
![]() 的面积
的面积![]() ,
,
则四面体![]() 的体积
的体积![]() .
.
(3)设平面![]() 的法向量
的法向量![]() ,
,
 得
得![]() 得
得![]()
平面![]() 的法向量
的法向量![]() ,
,
设两法向量夹角![]() ,
, ,
,
所以所成锐二面角的大小为![]() .
.

练习册系列答案
相关题目
【题目】某同学在研究学习中,收集到某制药厂今年5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
| 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 6 | 8 |
若![]() 线性相关,线性回归方程为
线性相关,线性回归方程为![]() ,则以下为真命题的是( )
,则以下为真命题的是( )
A. ![]() 每增加1个单位长度,则
每增加1个单位长度,则![]() 一定增加0.7个单位长度
一定增加0.7个单位长度
B. ![]() 每增加1个单位长度,则
每增加1个单位长度,则![]() 必减少0.7个单位长度
必减少0.7个单位长度
C. 当![]() 时,
时,![]() 的预测值为8.1万盒
的预测值为8.1万盒
D. 线性回归直线![]() 经过点
经过点![]()