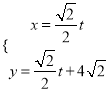Question

【题目】以下五个命题中：

①若，则的取值范围是；

②不等式，对一切x恒成立，则实数的取值范围为；

③若椭圆的两焦点为、，且弦过点，则的周长为16；

④若常数，，，成等差数列，则，，成等比数列；

⑤数列的前项和为=+2－1，则这个数列一定是等差数列.

所有正确命题的序号是_____________.

Answer 1

【答案】④

【解析】

对于①由不等式性质可判断;对于②讨论当和两种情况,即可判断;对于③根据椭圆方程求得,求得的周长, 即可作出判断;对于④由等差中项与等比中项定义和性质,即可判断;对于⑤根据数列中,结合首项即可判断数列是否为等差数列.

对于①,,则,所以,故①错误;

对于②,当时,不等式变为,对一切x恒成立,所以成立;当时,由二次函数的性质可知,解得.综上可知,故②错误;

对于③,椭圆.则.弦过点,则的周长为,故③错误;

对于④,,,成等差数列则.常数,则,所以,,成等比数列,故④正确;

对于⑤,数列的前项和为,当时,代入解得.当时,由可得,化简可得.且,所数列是从第二项开始的等差数列.故⑤错误.

综上可知,正确的为④.

故答案为: ④