题目内容
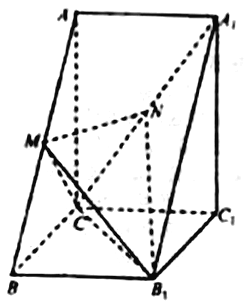
【题目】如图,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
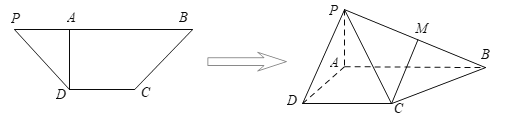
(1)若![]() 是侧棱
是侧棱![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,再根据线面平行的判定定理即可证明
,再根据线面平行的判定定理即可证明![]() 平面
平面![]() ;
;
(2)先利用面面垂直的性质定理得出![]() 平面
平面![]() ,建立空间坐标系,求出平面
,建立空间坐标系,求出平面![]() 的法向量,利用向量法即可求直线
的法向量,利用向量法即可求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() ,且
,且![]() ,
,
则四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)∵![]() ,平面
,平面![]() 平面
平面![]() ,面
,面![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴,建立空间直角坐标系如图:
轴,建立空间直角坐标系如图:
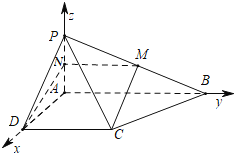
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则由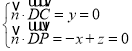 ,令
,令![]() ,则
,则![]() ,即
,即![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则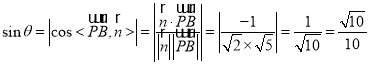 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: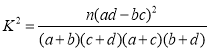
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16