题目内容
9.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则点C到平面BC1D的距离等于( )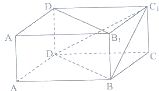
| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
分析 利用几何体作出点C到平面BC1D的距离的线段,然后求解即可.
解答 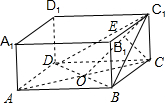 解:如图,连结BD,AC 交点为O,连结OC1,作CE⊥OC1于E,
解:如图,连结BD,AC 交点为O,连结OC1,作CE⊥OC1于E,
∵在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,
∴△BDC1是等腰三角形,DC1=C1B=$\sqrt{5}$,BD=2$\sqrt{2}$,
OC1=$\sqrt{3}$,
OC=$\sqrt{2}$,
长方体的底面是正方形,AC⊥BD,易知BD⊥平面OC1C,
则CE⊥C1O,点C到平面BC1D的距离等于CE,
CE=$\frac{OC•{CC}_{1}}{{OC}_{1}}$=$\frac{\sqrt{2}•1}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,
故选:C.
点评 本题考查点到平面的距离的求法,作出所求距离的相等是解题的关键,考查空间想象能力以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.设$a={(\frac{2}{3})^x}$,$b={(\frac{3}{2})^{x-1}}$,$c={log_{\frac{2}{3}}}x$,若x>1,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的两条渐近线与以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为圆心、半径为$\frac{16}{5}$的圆相切,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |
4.下列函数中是偶函数,且最小正周期是π的函数是( )
| A. | y=tanx | B. | y=sinx | C. | y=sin($\frac{3π}{2}$-2x) | D. | y=cos(π-x) |
14.设集合A={x|x2+3x<0},B={x|x<-1},则A∩B=( )
| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|x<-1} | D. | {x|x>0} |
18.设数列{an}满足an+1+an-1≤2an(n∈N*,n≥2),则称数列{an}为凸数列,已知等差数列{bn}的公差为lnd,首项b1=2,且数列{$\frac{{b}_{n}}{n}$}为凸数列,则d的取值范围是( )
| A. | (0,e2] | B. | [e2,+∞) | C. | (2,e2] | D. | [2,+∞) |
6.设α,β,γ是三个互不重合的平面,m,n是两条不重合的直线,下列命题中正确的是( )
| A. | 若α⊥β,β⊥γ,则α⊥γ | B. | 若m∥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α⊥β,m?β,m⊥α,则m∥β | D. | 若α∥β,m∥α,则m∥β |