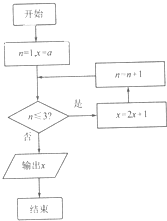
题目内容
4.下列函数中是偶函数,且最小正周期是π的函数是( )| A. | y=tanx | B. | y=sinx | C. | y=sin($\frac{3π}{2}$-2x) | D. | y=cos(π-x) |
分析 由条件利用三角函数的周期性和奇偶性逐一判断各个选项中函数的周期性和奇偶性,从而得出结论.
解答 解:由于y=tanx为奇函数,故不满足条件,故排除A;由于y=sinx为奇函数,故不满足条件,故排除B;
由于函数y=sin($\frac{3π}{2}$-2x)=-cos2x,故函数的周期为π,且是偶函数,满足条件;
由于y=cos(π-x)=cosx,它的周期为2π,故不满足条件,故排除D,
故选:C.
点评 本题主要考查诱导公式,三角函数的周期性和奇偶性,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
9.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则点C到平面BC1D的距离等于( )


| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
16.若a,b∈R,那么“a<b<0”是“$\frac{1}{a}>\frac{1}{b}$”成立的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
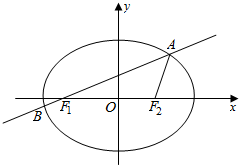 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.