题目内容
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的两条渐近线与以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为圆心、半径为$\frac{16}{5}$的圆相切,则双曲线的离心率为( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |
分析 求出双曲线的渐近线方程,求出圆的圆心坐标,利用圆心到直线的距离等于半径求解关系式,即可得到双曲线的离心率.
解答 解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为圆心(-4,0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的两条渐近线为:y=±$\frac{3}{a}$x,
双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的两条渐近线与以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为圆心、半径为$\frac{16}{5}$的圆相切,
可得:$\frac{\left|\frac{12}{a}\right|}{\sqrt{1+{(\frac{3}{a})}^{2}}}=\frac{16}{5}$,
解得a=$\frac{9}{4}$,
c=$\sqrt{\frac{81}{16}+9}$=$\frac{15}{4}$.
双曲线的离心率为:$\frac{\frac{15}{4}}{\frac{9}{4}}$=$\frac{5}{3}$.
故选:B.
点评 本题考查圆的方程的应用,椭圆与双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
7.若不等式x2-ax+a≤1有解,则a的取值范围为( )
| A. | a<2 | B. | a=2 | C. | a>2 | D. | a∈R |
8.已知tanα,tanβ是关于x的方程x2+(logaM+logbM)x-logaM•logbM=0两个根,其中a,b,M均不为1的正数,若sinαcosβ+cosαsinβ=2sinαsinβ,则a,b,M满足的关系是( )
| A. | $\frac{a+b}{2}$=M | B. | $\sqrt{ab}$=M | C. | a+b=M | D. | ab=M |
5.已知f(x)是R上的奇函数,且当x∈(-∞,0]时,f(x)=-xlg(2m-x+$\frac{1}{2}$).当x>0时,不等式f(x)<0恒成立,则m的取值范围是( )
| A. | (-∞,-1) | B. | (-1,1] | C. | [0,+∞) | D. | [-1,+∞) |
2.已知tanα=$\frac{2}{5}$,tanβ=$\frac{1}{4}$,则tan(α-β)等于( )
| A. | $\frac{13}{18}$ | B. | $\frac{13}{22}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{22}$ |
9.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则点C到平面BC1D的距离等于( )
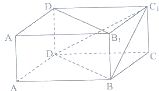

| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
 如图,抛物线C的顶点为坐标原点,焦点F为圆x2+(y-1)2=1的圆心.
如图,抛物线C的顶点为坐标原点,焦点F为圆x2+(y-1)2=1的圆心.