题目内容
1.已知正数x,y满足:x+4y=xy,则x+y的最小值为9.分析 将x+4y=xy,转化为$\frac{4}{x}$+$\frac{1}{y}$=1,再由x+y=(x+y)($\frac{4}{x}$+$\frac{1}{y}$)展开后利用基本不等式可求出x+y的最小值.
解答 解:∵x>0,y>0,x+4y=xy,
∴$\frac{4}{x}$+$\frac{1}{y}$=1,
∴x+y=(x+y)($\frac{4}{x}$+$\frac{1}{y}$)=5+$\frac{x}{y}$+$\frac{4y}{x}$≥5+2$\sqrt{\frac{x}{y}•\frac{4y}{x}}$=9,当且仅当x=2y取等号,结合x+4y=xy,
解得x=6,y=3
∴x+y的最小值为9,
故答案为:9.
点评 本题考查基本不等式,应注意等号成立的条件;“1”的替换是一个常用的技巧,应学会灵活运用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
11.河南省2013级高中学业水平考试在2015年1月16日至18日共考试三天,需考语文、数学、英语、物理、化学、生物、政治、历史、地理九门学科,若语文、数学、英语必须安排在下午,每天上午安排其余的六门学科,且每天上午考两门,下午考一门,问有多少种安排考试顺序的方法( )
| A. | 540 | B. | 720 | C. | 3240 | D. | 4320 |
9.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则点C到平面BC1D的距离等于( )
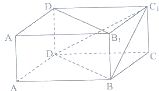

| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
16.若a,b∈R,那么“a<b<0”是“$\frac{1}{a}>\frac{1}{b}$”成立的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
10.函数f(x)=x2-1,则f(1)=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
 如图,抛物线C的顶点为坐标原点,焦点F为圆x2+(y-1)2=1的圆心.
如图,抛物线C的顶点为坐标原点,焦点F为圆x2+(y-1)2=1的圆心.