Question

【题目】已知抛物线（），过点（）的直线与交于、两点.

（1）若，求证：是定值（是坐标原点）；

（2）若（是确定的常数），求证：直线过定点，并求出此定点坐标；

（3）若的斜率为1，且，求的取值范围.

Answer 1

【答案】（1）定值为，证明见解析；（2）证明见解析；定点；（3）.

【解析】

（1）a时，设过点M的直线l为x＝ty，与抛物线方程联立消去x，得关于y的一元二次方程，由根与系数的关系和数量积的坐标运算即可求出为定值；

（2）设出直线AB的方程为x＝ty+n，与抛物线方程联立消去x，得关于y的一元二次方程，由根与系数的关系得出y1y2的值，再由题意列出方程求出n的值，即可得出直线AB过定点；

（3）由题意写出直线AB的方程为y＝x﹣a，与抛物线方程联立消去y，得关于x的一元二次方程，由根与系数的关系以及判别式△＞0，即可求出a的取值范围．

解：（1）当a时，点M（，0），

设直线l：x＝ty，

由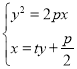，消去x，得

y2﹣2pty﹣p2＝0，

所以y1y2＝﹣p2，

则x1x2；

x1x2+y1y2p2为定值；

（2）设直线AB：x＝ty+n，

由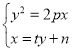，消去x，得

y2﹣2pty﹣2pn＝0，

所以y1y2＝﹣2pn，

又y1y2＝m，则﹣2pn＝m，即n；

则直线AB过定点（，0）；

（3）由题意：直线AB的方程为：y＝x﹣a，

代入抛物线得：x2﹣2（a+p）x+a2＝0，

由△＝4（a+p）2﹣4a2＞0得：a；

x1+x2＝2（a+p），x1x2＝a2，

所以|AB||x1﹣x2|＝22p，

解得a；

所以a的取值范围是（，]．