题目内容
8.(Ⅰ) 化简:$\frac{sin(π-α)cos(2π-α)tan(-α+π)}{-tan(-π-α)sin(-π-α)}$;(Ⅱ)已知α为第二象限的角,化简:$cosα\sqrt{\frac{1-sinα}{1+sinα}}+sinα\sqrt{\frac{1-cosα}{1+cosα}}$.
分析 (Ⅰ) 利用三角函数的诱导公式化简;
(Ⅱ)利用三角函数的基本关系式对代数式变形、化简.
解答 解:(Ⅰ)$\frac{sin(π-α)cos(2π-α)tan(-α+π)}{-tan(-π-α)sin(-π-α)}$=$\frac{sinαcosαtan(-α)}{tan(π+α)[-sin(π+α)]}$=$\frac{-sinαcosαtanα}{tanαsinα}$=-cosα.
(Ⅱ)$cosα\sqrt{\frac{1-sinα}{1+sinα}}+sinα\sqrt{\frac{1-cosα}{1+cosα}}$=$cosα\sqrt{\frac{{{{({1-sinα})}^2}}}{{1-{{sin}^2}α}}}+sinα\sqrt{\frac{{{{({1-cosα})}^2}}}{{1-{{cos}^2}α}}}$•=$cosα\frac{1-sinα}{{|{cosα}|}}+sinα\frac{1-cosα}{{|{sinα}|}}$.
∵α是第二象限角,∴cosα<0,sinα>0
上式=cosα×$\frac{1-sinα}{-cosα}$+$sinα×\frac{1-cosα}{sinα}$=sinα-1+1-cosα=sinα-cosα=$\sqrt{2}$sin($α-\frac{π}{4}$).
点评 本题考查了利用三角函数诱导公式以及基本关系式化简三角函数式;注意三角函数符号以及名称.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
18.一个蜂巢里有1只蜜蜂,第1天,它飞出去找回了3个伙伴;第2天,4只蜜蜂飞出去,各自找回了3个伙伴如果这个找伙伴的过程继续下去,第6天所有的蜜蜂都归巢后,蜂巢中蜜蜂的总只数为( )
| A. | 243 | B. | 729 | C. | 1024 | D. | 4096 |
3.在△ABC中,已知$\overrightarrow{AB}$=(cos18°,cos72°),$\overrightarrow{BC}$=(2cos63°,2cos27°),则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
13.抛物线y=$\frac{1}{4}$x2的准线方程是( )
| A. | $x=-\frac{1}{16}$ | B. | $x=-\frac{1}{8}$ | C. | y=-1 | D. | y=-2 |
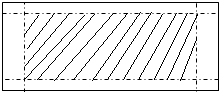 为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小?
为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小?