题目内容
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)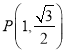 (Ⅱ)
(Ⅱ)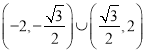
【解析】试题分析:(1)首先得到焦点的坐标,点![]() 满足两个条件,一个是点
满足两个条件,一个是点![]() 在椭圆上,满足椭圆方程,另一个是将
在椭圆上,满足椭圆方程,另一个是将![]() ,转化为坐标表示,这样两个方程两个未知数,解方程组;(2)首项设过点
,转化为坐标表示,这样两个方程两个未知数,解方程组;(2)首项设过点![]() 的直线为
的直线为![]() ,与方程联立,得到根与系数的关系,
,与方程联立,得到根与系数的关系, ![]() 和
和![]() ,以及
,以及![]() ,根据向量的数量积可知,
,根据向量的数量积可知, ![]() 为锐角,即
为锐角,即![]() ,这样代入根与系数的关系,以及
,这样代入根与系数的关系,以及![]() ,共同求出
,共同求出![]() 的取值范围.
的取值范围.
试题解析:(1)易知![]() .
.
![]() ,设
,设![]() ,则
,则
![]() ,又
,又![]() .
.
联立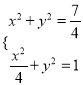 ,解得
,解得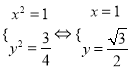 ,故
,故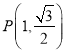 .
.
(2)显然![]() 不满足题设条件,可设
不满足题设条件,可设![]() 的方程为
的方程为![]() ,
,
设![]() ,
,
联立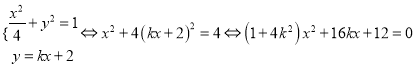
![]()
由![]()
![]() ,得
,得![]() .①
.①
又![]() 为锐角
为锐角![]() ,
,
![]()
又![]()
![]()
![]() .②
.②
综①②可知![]() 的取值范围是
的取值范围是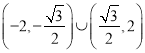

练习册系列答案
相关题目