题目内容
3.已知在△ABC中,a=2,∠A=$\frac{π}{3}$.(1)求面积的最大值;
(2)求周长的最大值;
(3)若三角形为锐角三角形,求周长的取值范围;
(4)求b+2c的取值范围;
(5)$\frac{sinB}{cosC}$>$\sqrt{3}$,求∠C的取值范围.
分析 (1)由余弦定理可得:a2=b2+c2-2bccosA,利用基本不等式的性质可得bc≤4.即可得出S△ABC=$\frac{1}{2}bcsinA$的最大值.
(2)由22=b2+c2-2bc$cos\frac{π}{3}$=(b+c)2-2bc-bc,利用基本不等式的性质可得b+c≤4,即可得出a+b+c的最大值.
(3)由正弦定理可得a+b+c=2+$\frac{4}{\sqrt{3}}$(sinB+sinC)=2+4$sin(C+\frac{π}{6})$,由$C+B=\frac{2π}{3}$,$0<C,B<\frac{π}{2}$,可得$\frac{π}{3}<C+\frac{π}{6}<\frac{2π}{3}$,即可得出;
(4)由正弦定理可得b+2c=$\frac{4}{\sqrt{3}}(sinB+2sinC)$=$\sqrt{7}$sin(C+θ),其中sinθ=$\frac{\sqrt{21}}{14}$,$cosθ=\frac{5\sqrt{7}}{14}$,tanθ=$\frac{\sqrt{3}}{5}$.由$C∈(0,\frac{2π}{3})$,可得sin(C+θ)∈$(\frac{\sqrt{21}}{14},1]$,即可得出.
(5)由$\frac{sinB}{cosC}$>$\sqrt{3}$,B=$\frac{2π}{3}-C$,可得$0<C<\frac{π}{2}$,化为$sin(C-\frac{π}{3})$>0,进而得出.
解答 解:(1)由余弦定理可得:a2=b2+c2-2bccosA,∴22=b2+c2-2bc$cos\frac{π}{3}$≥2bc-bc=bc,当且仅当b=c时取等号,即bc≤4.
∴S△ABC=$\frac{1}{2}bcsinA$$≤\frac{1}{2}×\frac{\sqrt{3}}{4}×4$=$\frac{\sqrt{3}}{2}$.∴S△ABC的最大值为$\frac{\sqrt{3}}{2}$.
(2)∵22=b2+c2-2bc$cos\frac{π}{3}$=(b+c)2-2bc-bc≥(b+c)2$-3×(\frac{b+c}{2})^{2}$,化为b+c≤4,当且仅当b=c=2时取等号.
∴a+b+c≤2+4=6,因此周长的最大值为:6.
(3)由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=$\frac{2}{sin\frac{π}{3}}$=$\frac{4}{\sqrt{3}}$,
∴a+b+c=2+$\frac{4}{\sqrt{3}}$(sinB+sinC)=2+$\frac{4}{\sqrt{3}}$$[sin(\frac{2π}{3}-C)+sinC]$=2+4$sin(C+\frac{π}{6})$,∵$C+B=\frac{2π}{3}$,$0<C,B<\frac{π}{2}$,∴$\frac{π}{6}<C<\frac{π}{2}$,∴$\frac{π}{3}<C+\frac{π}{6}<\frac{2π}{3}$,∴$\frac{\sqrt{3}}{2}<sin(C+\frac{π}{6})$≤1,∴(a+b+c)∈$(2+2\sqrt{3},6]$.
(4)由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=$\frac{2}{sin\frac{π}{3}}$=$\frac{4}{\sqrt{3}}$,
∴b+2c=$\frac{4}{\sqrt{3}}(sinB+2sinC)$=$\frac{4}{\sqrt{3}}[sin(\frac{2π}{3}-C)+2sinC]$=$\sqrt{7}$$(\frac{\sqrt{21}}{14}cosC+\frac{5\sqrt{7}}{14}sinC)$=$\sqrt{7}$sin(C+θ),其中sinθ=$\frac{\sqrt{21}}{14}$,$cosθ=\frac{5\sqrt{7}}{14}$,tanθ=$\frac{\sqrt{3}}{5}$.
∵$C∈(0,\frac{2π}{3})$,∴(C+θ)∈$(arctan\frac{\sqrt{3}}{5},\frac{2π}{3}+arctan\frac{\sqrt{3}}{5})$,∴sin(C+θ)∈$(\frac{\sqrt{21}}{14},1]$,∴(b+2c)∈$(\frac{\sqrt{3}}{2},\sqrt{7}]$.
(5)∵$\frac{sinB}{cosC}$>$\sqrt{3}$,B=$\frac{2π}{3}-C$,
∴$0<C<\frac{π}{2}$,$sin(\frac{2π}{3}-C)>\sqrt{3}$cosC,
化为$sin(C-\frac{π}{3})$>0,
∴$\frac{π}{3}<C<\frac{π}{2}$.即C∈$(\frac{π}{3},\frac{π}{2})$.
点评 本题考查了正弦定理余弦定理、三角形的周长与面积的最值问题、基本不等式的性质、两角和差公式、三角函数的单调性等基础知识与基本技能,考查了推理能力与计算能力,属于难题.

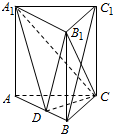 已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证:
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证: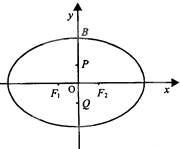 如图:设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右两个焦点分别为F1,F2,短轴的上端点为B,短轴上的两个三等分点为P,Q,且F1PF2Q为正方形,若过点B作此正方形的外接圆的切线在x轴上的一个截距为-$\frac{3\sqrt{2}}{4}$,则此椭圆方程的方程为$\frac{x^2}{10}+\frac{y^2}{9}=1$.
如图:设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右两个焦点分别为F1,F2,短轴的上端点为B,短轴上的两个三等分点为P,Q,且F1PF2Q为正方形,若过点B作此正方形的外接圆的切线在x轴上的一个截距为-$\frac{3\sqrt{2}}{4}$,则此椭圆方程的方程为$\frac{x^2}{10}+\frac{y^2}{9}=1$.