题目内容
2.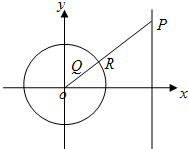 已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.
已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.(1)求圆C与直线l的极坐标方程;
(2)已知P是l上一动点,线段OP交圆C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2.当点P在l上移动时,求点Q在直角坐标系下的轨迹方程.
分析 (1)通过将x=ρcosθ、y=ρsinθ 分别代入圆C、直线l方程即可;
(2)通过设点Q(x,y),P(4,t),利用OP、OQ斜率相等即得P(4,4×$\frac{y}{x}$),结合|OR|=2、利用|OQ|•|OP|=|OR|2计算即可.
解答 解:(1)将x=ρcosθ、y=ρsinθ 代入圆C:x2+y2=4,
可得:ρ2=4,
即圆C的极坐标方程为:ρ=2;
将x=ρcosθ、y=ρsinθ 代入直线l:x=8,
可得l的极坐标方程为:ρcosθ=8;
(2)设点Q(x,y),P(4,t),显然x>0,
∵P、Q共线,
∴P、Q为同一角的终边上,
∵直线l:x=8,
∴$\frac{y}{x}$=$\frac{t}{4}$,∴P(4,4×$\frac{y}{x}$),
又∵R在圆C:x2+y2=4上,
∴|OR|=2,
∵|OQ|•|OP|=|OR|2,
∴$\sqrt{{x}^{2}+{y}^{2}}$•$\sqrt{{4}^{2}+(\frac{4y}{x})^{2}}$=22,
整理得:x2-x+y2=0,
∴(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$(x>0),
∴点Q在直角坐标系下的轨迹方程为:(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$(x>0).
点评 本题主要考查坐标系与方程,直线、椭圆的方程和性质,曲线与方程的关系,轨迹的概念和求法,利用方程判定曲线的性质等解析几何的基本思想和综合运用知识的能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.已知两座灯塔A、B与灯塔C的距离分别为1km,2km.灯塔A在C的北偏东20°,灯塔B在C的南偏东40°,则灯塔A与B的距离为( )km.
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
13.若某几何体的三视图 (单位:cm) 如图所示,则此几何体的表面积是(cm2)( )

| A. | 2$\sqrt{13}$π+6 | B. | 2π+6 | C. | $6+(2\sqrt{13}+2)π$ | D. | $6+(\sqrt{13}+2)π$ |
7.现有如下投资方案,一年后投资盈亏的情况如下:
(1)投资股市:
(2)购买基金:
(Ⅰ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于$\frac{4}{5}$,求p的取值范围;
(Ⅱ)丙要将家中闲置的20万元钱进行投资,决定在“投资股市”、“购买基金”,或“等额同时投资股市和购买基金”这三种方案中选择一种,已知$p=\frac{1}{2}$,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?(其中第三方案须考察两项获利之和的随机变量Z),给出结果并说明理由.
(1)投资股市:
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ | q |
(Ⅱ)丙要将家中闲置的20万元钱进行投资,决定在“投资股市”、“购买基金”,或“等额同时投资股市和购买基金”这三种方案中选择一种,已知$p=\frac{1}{2}$,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?(其中第三方案须考察两项获利之和的随机变量Z),给出结果并说明理由.
9.函数y=x3-3x在(m,6-m2)上有最小值,则实数m的取值范围是( )
| A. | (-$\sqrt{5}$,1) | B. | [-$\sqrt{5}$,1) | C. | [-2,1) | D. | (-2,1) |
 已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R
已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R