题目内容
9. 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.
分析 连接DE,证明△DBE∽△CBA,利用AB=2AC,结合角平分线性质,即可证明BE=2AD,根据割线定理得BD•BA=BE•BC,从而可求AD的长.
解答 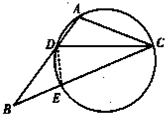 解:连接DE,
解:连接DE,
∵ACED是圆内接四边形,
∴∠BDE=∠BCA,
又∠DBE=∠CBA,∴△DBE∽△CBA,即有$\frac{BE}{BA}=\frac{DE}{CA}$,
又∵AB=2AC,∴BE=2DE,
∵CD是∠ACB的平分线,∴AD=DE,
∴BE=2AD,
设AD=t,则BE=2t,BC=2t+6,
根据割线定理得BD•BA=BE•BC,
即(6-t)×6=2t•(2t+6),即2t2+9t-18=0,
解得t=$\frac{3}{2}$或-6(舍去),则AD=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查三角形相似,考查角平分线性质、割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.设m,n是不同的直线,α,β是不同的平面,已知m∥α,n⊥β,下列说法正确的是( )
| A. | 若m⊥n,则α⊥β | B. | 若m∥n,则α⊥β | C. | 若m⊥n,则α∥β | D. | 若m∥n,则α∥β |
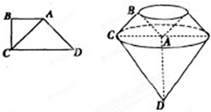 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体
