题目内容
【题目】(导学号：05856334)
已知函数f(x)＝ln x＋ax2＋1.
(Ⅰ)当a＝－1时，求函数f(x)的极值；
(Ⅱ)当a>0时，证明：存在正实数λ，使得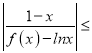
λ恒成立．
【答案】(1) 函数f(x)有极大值
，无极小值(2)见解析
【解析】试题分析：（1）运用求解导数得出f′（x）=
+2ax，x＞0，判断（0， 
）单调递增，（ 
，+∞）单调递减，
得出f（x）极大值=f（
）=ln
+
，无极小值．
（2）构造g（x）=
，当a＞0时g（x）的定义域为R，
g′（x）=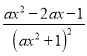
，g′（x）=
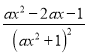=0，x1=1
，x2=1
，
判断得出g（x）在（﹣∞，x1）（x2，+∞）单调递增，（1，2）单调递减，求解得出极值，得出存在常数M，得出不等式恒成立．
试题解析：
(Ⅰ)依题意，f(x)＝ln x－x2＋1，x∈(0，＋∞)，f′(x)＝
＝
，
故当x∈(0，
)时，f′(x)>0，
当x∈(，＋∞)时，f′(x)<0，
故函数f(x)有极大值f()＝ln－＋1＝－ln 2＋，无极小值.
(Ⅱ)令g(x)＝
＝
(x＞0，a＞0)，
g′(x)＝
，令g′(x)＝0，解得x1＝1－
<0(舍去)，x2＝1＋>1，
当x变化时，g′(x)与g(x)的变化情况如下表：
x | (0，x2) | x2 | (x2，＋∞) |
g′(x) | － | 0 | ＋ |
g(x) | ↘ | ↗ |
所以函数g(x)在(x2，＋∞)上单调递增，在(0，x2)上单调递减．
又因为g(1)＝0，当0＜x<1时，g(x)＝>0；当x>1时，g(x)＝<0，
所以当0＜x≤1时，0≤g(x)＜g(0)＝1；当x>1时，g(x2)≤g(x)<0.
记M为1，|g(x2)|中最大的数，则||≤λ恒成立M≤λ.
综上，当a>0时，存在正实数λ∈[M，＋∞)，使得对任意的实数x，不等式||≤λ恒成立.
练习册系列答案
相关题目
