题目内容
设函数 .
.
(1)若 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和 的极大值;
的极大值;
(2)若 在定义域上是增函数,求实数
在定义域上是增函数,求实数 的取值范围.
的取值范围.
 .
.(1)若
 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和 的极大值;
的极大值;(2)若
 在定义域上是增函数,求实数
在定义域上是增函数,求实数 的取值范围.
的取值范围.(1)极大值为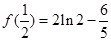 (2)
(2)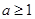
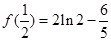 (2)
(2)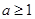
试题分析:(1)先求导,根据
 在
在 时有极值,则
时有极值,则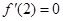 ,可求得
,可求得 的值。代入导数解析式并整理,令导数大于0可得增区间,令导数小于0可得减区间。根据单调性可求极值。(2)
的值。代入导数解析式并整理,令导数大于0可得增区间,令导数小于0可得减区间。根据单调性可求极值。(2) 在定义域上是增函数,则当
在定义域上是增函数,则当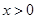 时
时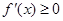 恒成立。因为
恒成立。因为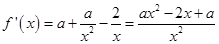 ,且
,且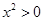 ,所以只需
,所以只需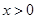 时
时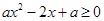 ,即
,即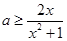 恒成立。可用基本不等式求
恒成立。可用基本不等式求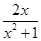 的最大值则
的最大值则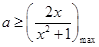 。
。(1)∵
 在
在 时有极值,∴有
时有极值,∴有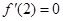
又
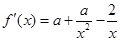 ∴
∴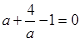 ,∴
,∴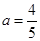 2分
2分∴有
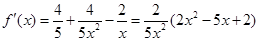
由
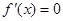 得
得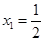 ,
,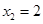
又
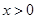 ∴由
∴由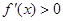 得
得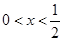 或
或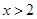
由
 得
得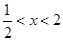
∴
 在区间
在区间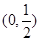 和
和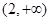 上递增,在区间
上递增,在区间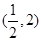 上递减 5分
上递减 5分∴
 的极大值为
的极大值为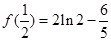 6分
6分(2)若
 在定义域上是增函数,则
在定义域上是增函数,则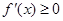 在
在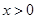 时恒成立
时恒成立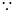
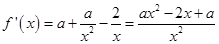 ,
,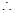 需
需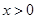 时
时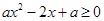 恒成立, 9分
恒成立, 9分化
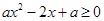 为
为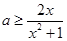 恒成立,
恒成立,
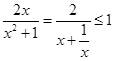 ,
,
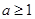 为所求。 12分
为所求。 12分
练习册系列答案
相关题目
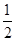 ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度;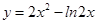 的的单调递减区间是 。
的的单调递减区间是 。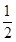 ,求F(x)=f(x)-g(x)的单调区间;
,求F(x)=f(x)-g(x)的单调区间; 在
在 为单调增函数,则实数
为单调增函数,则实数 的取值范围为( )
的取值范围为( )



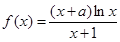 ,曲线
,曲线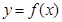 在点
在点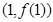 处的切线与直线
处的切线与直线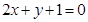 垂直.
垂直.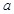 的值;
的值;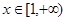 ,
,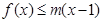 恒成立,求
恒成立,求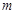 的范围;
的范围;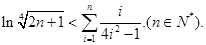
 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于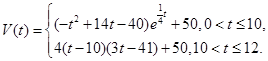
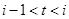 表示第1月份(
表示第1月份( ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?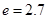 计算).
计算). 在区间
在区间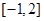 上是减函数,那么
上是减函数,那么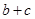 的最大值为 .
的最大值为 .