题目内容
设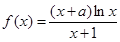 ,曲线
,曲线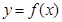 在点
在点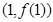 处的切线与直线
处的切线与直线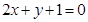 垂直.
垂直.
(1)求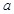 的值;
的值;
(2)若对于任意的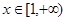 ,
,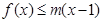 恒成立,求
恒成立,求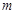 的范围;
的范围;
(3)求证: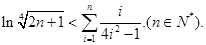
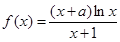 ,曲线
,曲线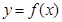 在点
在点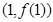 处的切线与直线
处的切线与直线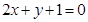 垂直.
垂直.(1)求
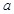 的值;
的值;(2)若对于任意的
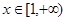 ,
,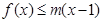 恒成立,求
恒成立,求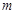 的范围;
的范围;(3)求证:
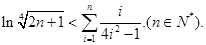
试题分析:(1)求得函数f(x)的导函数,利用曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直,即可求a的值;
(2)先将原来的恒成立问题转化为lnx≤m(x?
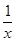 ),设g(x)=lnx?m(x?
),设g(x)=lnx?m(x?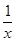 ),即?x∈(1,+∞),g(x)≤0.利用导数研究g(x)在(0,+∞)上单调性,求出函数的最大值,即可求得实数m的取值范围.
),即?x∈(1,+∞),g(x)≤0.利用导数研究g(x)在(0,+∞)上单调性,求出函数的最大值,即可求得实数m的取值范围.(3)由(2)知,当x>1时,m=
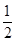 时,lnx<
时,lnx<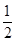 (x?
(x?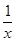 )成立.不妨令x=
)成立.不妨令x=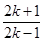 ,k∈N*,得出
,k∈N*,得出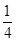 [ln(2k+1)?ln(2k?1)]<
[ln(2k+1)?ln(2k?1)]<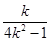 ,k∈N*,再分别令k=1,2,,n.得到n个不等式,最后累加可得.
,k∈N*,再分别令k=1,2,,n.得到n个不等式,最后累加可得.(1)
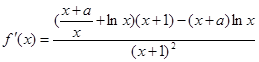 2分
2分由题设
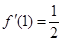 ,∴
,∴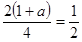
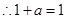 ,
,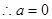 . 4分
. 4分(2)
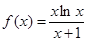 ,
,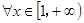 ,
,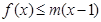 ,即
,即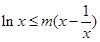
设
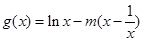 ,即
,即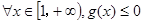 .
.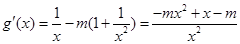 6分
6分①若
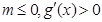 ,
,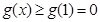 ,这与题设
,这与题设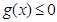 矛盾. 7分
矛盾. 7分②若
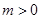 方程
方程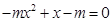 的判别式
的判别式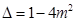
当
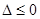 ,即
,即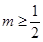 时,
时, .
.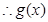 在
在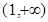 上单调递减,
上单调递减,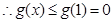 ,即不等式成立. 8分
,即不等式成立. 8分当
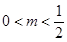 时,方程
时,方程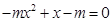 ,设两根为
,设两根为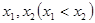
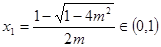 ,
,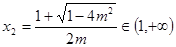
当
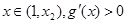 ,
,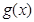 单调递增,
单调递增,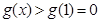 ,与题设矛盾.
,与题设矛盾.综上所述,
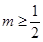 . 10分
. 10分(3) 由(2)知,当
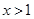 时,
时, 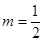 时,
时,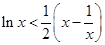 成立.
成立.不妨令
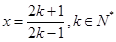
所以
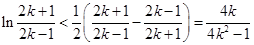 ,
,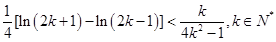 11分
11分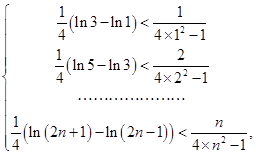 12分
12分累加可得
∴
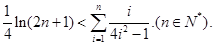
∴
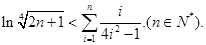 ---------------14分
---------------14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和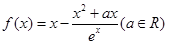 .
. 时,证明:当
时,证明:当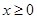 时,
时,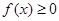 ;
;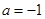 时,证明:
时,证明: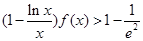 .
.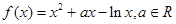 .
.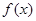 的单调区间;
的单调区间;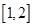 上是减函数,求实数a的取值范围;
上是减函数,求实数a的取值范围;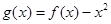 ,是否存在实数a,当
,是否存在实数a,当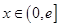 (e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.
(e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.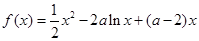 ,
,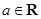 .
. 时,求函数
时,求函数 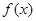 的最小值;
的最小值; 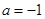 时,求证:无论
时,求证:无论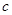 取何值,直线
取何值,直线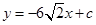 均不可能与函数
均不可能与函数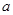 ,对任意的
,对任意的 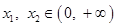 ,且
,且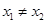 ,有
,有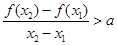 恒成立,若存在求出
恒成立,若存在求出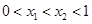 ,则( )
,则( )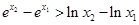
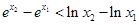
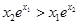
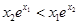
 的导函数
的导函数 的图像如图所示,则( )
的图像如图所示,则( )
 为
为 为
为 为
为 为
为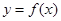 的导函数
的导函数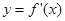 的图象,给出下列命题:
的图象,给出下列命题: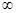 ,-2)上单调递减
,-2)上单调递减
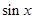 在(0,2π)上是( )
在(0,2π)上是( )