题目内容
已知函数f(x)=(x-a)(x-b)2,a,b是常数.
(1)若a≠b,求证:函数f(x)存在极大值和极小值;
(2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1,x2,设点A(x1,f(x1)),B(x2,f(x2)).如果直线AB的斜率为-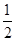 ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度;
(3)若f(x)≥mxf′(x)对于一切x∈R恒成立,求实数m,a,b满足的条件.
(1)若a≠b,求证:函数f(x)存在极大值和极小值;
(2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1,x2,设点A(x1,f(x1)),B(x2,f(x2)).如果直线AB的斜率为-
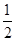 ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度;(3)若f(x)≥mxf′(x)对于一切x∈R恒成立,求实数m,a,b满足的条件.
(1)见解析 (2)公共减区间为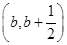 或
或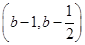 ,长度均为
,长度均为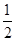
(3)m=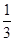 ,a=b≤0.
,a=b≤0.
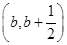 或
或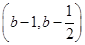 ,长度均为
,长度均为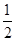
(3)m=
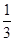 ,a=b≤0.
,a=b≤0.解:(1)证明:
f′(x)=(x-b)[3x-(2a+b)],
因为a≠b,所以b≠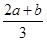 ,
,
所以f′(x)=0有两个不等实根b和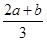 ,
,
所以f(x)存在极大值和极小值.
(2)①当a=b时,f(x)不存在减区间;
②当a>b时,由(1)知x1=b,x2=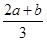 ,
,
所以A(b,0),B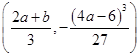 ,
,
所以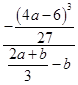 =-
=-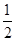 ,
,
即4(a-b)3=9(a-b),
所以a-b=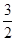 或a-b=-
或a-b=-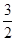 (舍去);
(舍去);
③当a<b时,x1=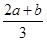 ,x2=b.
,x2=b.
同理可得a-b=-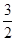 或a-b=
或a-b=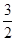 (舍去).
(舍去).
综上,a>b且a-b=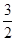 或a<b且a-b=-
或a<b且a-b=-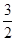 .
.
所以f(x)的减区间为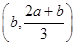 ,即(b,b+1)或f(x)的减区间为
,即(b,b+1)或f(x)的减区间为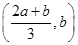 ,即(b-1,b);
,即(b-1,b);
f′(x)的减区间为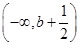 或
或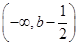 .
.
所以公共减区间为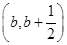 或
或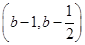 ,长度均为
,长度均为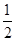 .
.
(3)由题意f(x)≥mxf′(x),
所以(x-a)(x-b)2≥mx(x-b)[3x-(2a+b)],
所以(x-b){(1-3m)x2+[m(2a+b)-(a+b)]x+ab}≥0.
若m≠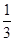 ,则左边是一个一次因式乘一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负.
,则左边是一个一次因式乘一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负.
所以m=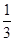 ,
,
所以(x-b)[(a+2b)x-3ab]≤0.
若a+2b=0,则a=-2b,所以a=b=0;
若a+2b≠0,则x1=b,x2=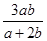 ,
,
所以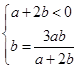
①若b=0,则a<0;
②若b≠0,则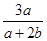 =1,所以a=b且b<0.
=1,所以a=b且b<0.
综上,m=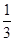 ,a=b≤0.
,a=b≤0.
f′(x)=(x-b)[3x-(2a+b)],
因为a≠b,所以b≠
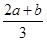 ,
,所以f′(x)=0有两个不等实根b和
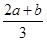 ,
,所以f(x)存在极大值和极小值.
(2)①当a=b时,f(x)不存在减区间;
②当a>b时,由(1)知x1=b,x2=
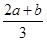 ,
,所以A(b,0),B
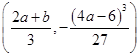 ,
,所以
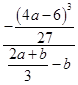 =-
=-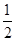 ,
,即4(a-b)3=9(a-b),
所以a-b=
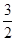 或a-b=-
或a-b=-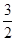 (舍去);
(舍去);③当a<b时,x1=
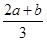 ,x2=b.
,x2=b.同理可得a-b=-
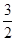 或a-b=
或a-b=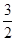 (舍去).
(舍去).综上,a>b且a-b=
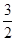 或a<b且a-b=-
或a<b且a-b=-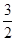 .
.所以f(x)的减区间为
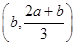 ,即(b,b+1)或f(x)的减区间为
,即(b,b+1)或f(x)的减区间为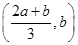 ,即(b-1,b);
,即(b-1,b);f′(x)的减区间为
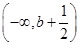 或
或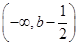 .
.所以公共减区间为
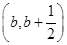 或
或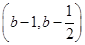 ,长度均为
,长度均为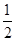 .
.(3)由题意f(x)≥mxf′(x),
所以(x-a)(x-b)2≥mx(x-b)[3x-(2a+b)],
所以(x-b){(1-3m)x2+[m(2a+b)-(a+b)]x+ab}≥0.
若m≠
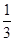 ,则左边是一个一次因式乘一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负.
,则左边是一个一次因式乘一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负.所以m=
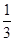 ,
,所以(x-b)[(a+2b)x-3ab]≤0.
若a+2b=0,则a=-2b,所以a=b=0;
若a+2b≠0,则x1=b,x2=
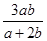 ,
,所以
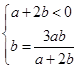
①若b=0,则a<0;
②若b≠0,则
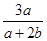 =1,所以a=b且b<0.
=1,所以a=b且b<0.综上,m=
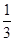 ,a=b≤0.
,a=b≤0.
练习册系列答案
相关题目
 .
. 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和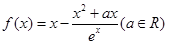 .
. 时,证明:当
时,证明:当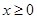 时,
时,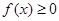 ;
;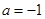 时,证明:
时,证明: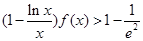 .
.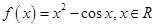 ,则( )
,则( )
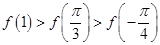
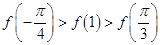
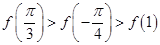
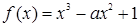 在
在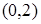 上单调递减,则实数
上单调递减,则实数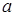 的取值范围为( )
的取值范围为( )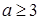
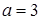
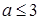
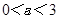
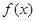 是定义在R上的奇函数,且
是定义在R上的奇函数,且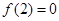 ,当x>0时,有
,当x>0时,有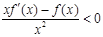 恒成立,则不等式
恒成立,则不等式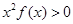 的解集是 ( )
的解集是 ( )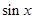 在(0,2π)上是( )
在(0,2π)上是( )