题目内容
【题目】从某高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于
和
之间，将测量结果按如下方式分成6组：第1组
，第2组
，…，第6组
，如图是按上述分组方法得到的频率分布直方图.
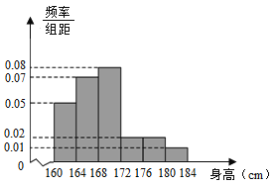
（1）由频率分布直方图估计该校高三年级男生身高的中位数；
（2）在这50名男生身高不低于
的人中任意抽取2人，则恰有一人身高在内的概率.
【答案】（1）
.（2）
【解析】
（1）由频率分布直方图得
频率为0.48，
的频率为0.32，由此能求出中位数.
（2）在这50名男生身高不低于
的人中任意抽取2人，
中的学生人数为4人，
中的学生人数为2人，可用列举法求出基本事件总数，恰有一人身高在
内包含的基本事件个数，再由概率公式计算出概率.
解：（1）由频率分布直方图得频率为：
，
的频率为：
，
∴中位数为：
.
（2）在这50名男生身高不低于的人中任意抽取2人，
中的学生人数为
人，编号为
，
中的学生人数为
人，编号为
，
任意抽取2人的所有基本事件为
，
，
，
共15个，
恰有一人身高在内包含的基本事件有
，
，
，
共8个，
∴恰有一人身高在内的概率
.
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
【题目】为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．
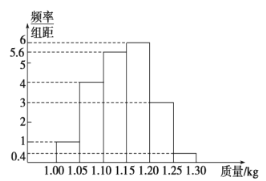
（1）在下面表格中填写相应的频率；
分组 | 频率 |
| |
| |
| |
| |
| |
|
（2）估计数据落在
中的概率；
（3）将上面捕捞的100条鱼分别作一记分组频率号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．
