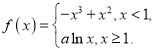题目内容
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).
(Ⅰ)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有![]() 的把握认为“该地区2017年家庭年收入与地区有关”?
的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()

【答案】(Ⅰ)45;(Ⅱ)![]() ;(Ⅲ)有
;(Ⅲ)有![]() 的把握认为“该地区2017年家庭年收入与地区有关”.
的把握认为“该地区2017年家庭年收入与地区有关”.
【解析】分析:(Ⅰ)利用分层抽样中每层所抽取的比例数相等求得答案;(Ⅱ)根据频率分布直方图可得该地区2017年家庭收入超过1.5万元的概率;(Ⅲ)由题意列出2×2列联表,计算出![]() 的值,结合附表得答案.
的值,结合附表得答案.
详解:(Ⅰ)由已知可得每户居民被抽取的概率为0.1,故应手机![]() 户山区家庭的样本数据.
户山区家庭的样本数据.
(Ⅱ)由直方图可知该地区2017年家庭年收入超过1.5万元的概率约为![]() .
.
(Ⅲ)样本数据中,年收入超过2万元的户数为![]() 户.
户.
而样本数据中,有5户山区家庭的年收入超过2万元,故列联表如下:
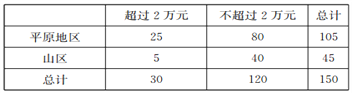
所以![]() ,
,
∴有![]() 的把握认为“该地区2017年家庭年收入与地区有关”.
的把握认为“该地区2017年家庭年收入与地区有关”.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】工厂车间某部门有8个小组,在一次技能考试中成绩情况分析如下:
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
大于90分人数 | 6 | 6 | 7 | 3 | 5 | 3 | 3 | 7 |
不大于90分人数 | 39 | 39 | 38 | 42 | 40 | 42 | 42 | 38 |
(1)求90分以上人数![]() 对小组序号
对小组序号![]() 的线性回归方程;
的线性回归方程;
附:回归方程为![]() ,其中
,其中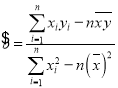 ,
,![]() .本题
.本题![]() ,
,![]() .
.
(2)能否在犯错误的概率不超过0.01的前提下认为7组与8组的成绩是否优秀(大于90分)与小组有关系.附部分临界值表:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
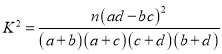 .
.
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: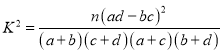 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|