Question

【题目】为了解共享单车在市的使用情况，某调查机构借助网络进行了问卷调查，并从参与调查的网友中随机抽取了人进行分析，得到如下列联表（单位：人）.

	经常使用	偶尔使用或不使用	合计
岁及以下
岁以上
合计

（1）根据以上数据，能否在犯错误的概率不超过的前提下认为市使用共享单车的情况与年龄有关；

（2）（i）现从所选取的岁以上的网友中，采用分层抽样的方法选取人，再从这人中随机选出人赠送优惠券，求选出的人中至少有人经常使用共享单车的概率；

（ii）将频率视为概率，从市所有参与调查的网友中随机选取人赠送礼品，记其中经常使用共享单车的人数为，求的数学期望和方差.

参考公式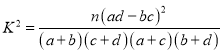：，其中.

参考数据：

Answer 1

【答案】（1）能；（2）（i）；（ii）数学期望为，方差为.

【解析】

（1）利用列联表中的数据计算出的观测值，再将观测值与进行大小比较，可对题中的结论进行判断；

（2）（i）先利用分层抽样方法计算出人中经常使用共享单车和偶尔使用或不使用共享单车的人数，然后利用古典概型的概率公式计算出所求事件的概率；

（ii）先由列联表计算出经常使用共享单车的网友的频率为，由题意得出随机变量服从于二项分布，利用二项分布的数学期望公式和方差公式可计算出结果.

（1）由列联表可知，，

，

能在犯错误的概率不超过的前提下认为市使用共享单车的情况与年龄有关；

（2）（i）依题意，可知所选取的名岁以上的网友中，

经常使用共享单车的有人，偶尔使用或不使用共享单车的有人.

则选出的人中至少有人经常使用共享单车的概率；

（ii）由列联表可知选到经常使用共享单车的网友频率为，

将频率视为概率，即从市所有参与调查的网友中任意选取人，恰好选到经常使用共享单车的网友的概率为.

由题意得，，.