题目内容
已知椭圆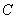 :
: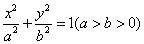 的一个顶点为
的一个顶点为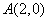 ,离心率为
,离心率为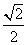 .直线
.直线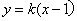 与椭圆
与椭圆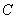 交于不同的两点M,N.
交于不同的两点M,N.
(Ⅰ)求椭圆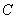 的方程;
的方程;
(Ⅱ)当△AMN得面积为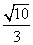 时,求
时,求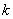 的值.
的值.
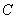 :
: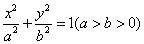 的一个顶点为
的一个顶点为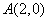 ,离心率为
,离心率为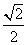 .直线
.直线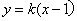 与椭圆
与椭圆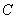 交于不同的两点M,N.
交于不同的两点M,N.(Ⅰ)求椭圆
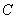 的方程;
的方程;(Ⅱ)当△AMN得面积为
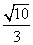 时,求
时,求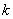 的值.
的值.(Ⅰ)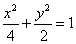 ;Ⅱ)
;Ⅱ)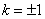
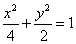 ;Ⅱ)
;Ⅱ)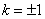
试题分析:(1)由题意得
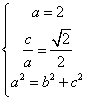 解得
解得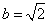 .所以椭圆C的方程为
.所以椭圆C的方程为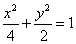 .
.(5分)
(2)由
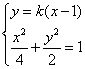 得
得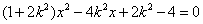 .(7分)
.(7分)设点M,N的坐标分别为
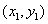 ,
, ,则
,则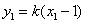 ,
,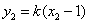 ,
,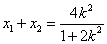 ,
, .(9分)
.(9分)所以|MN|=
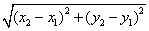 =
=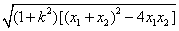 =
=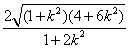 .
.由因为点A(2,0)到直线
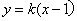 的距离
的距离 ,(10分)
,(10分)所以△AMN的面积为
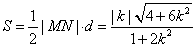 . 由
. 由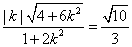 ,解得
,解得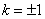 .(12分)
.(12分)点评:直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

练习册系列答案
相关题目
 轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)  平行于
平行于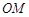 ,且与椭圆交于A、B两个不同点.
,且与椭圆交于A、B两个不同点.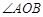 为钝角,求直线
为钝角,求直线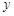 轴上的截距m的取值范围;
轴上的截距m的取值范围;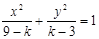 表示焦点在y轴上的双曲线,则k的取值范围是( )
表示焦点在y轴上的双曲线,则k的取值范围是( )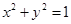 和定点A(2,1),由圆O外一点
和定点A(2,1),由圆O外一点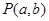 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足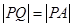
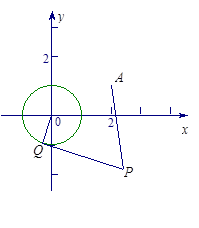
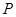 是以
是以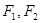 为左、右焦点的双曲线
为左、右焦点的双曲线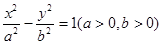 左支上一点,且满足
左支上一点,且满足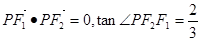 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )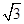
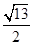
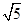
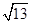
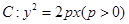 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.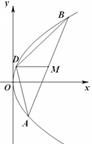
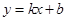 与抛物线C交于两点
与抛物线C交于两点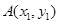 ,
,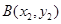 ,且
,且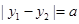 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到 .
.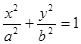 的左焦点作直线交椭圆于
的左焦点作直线交椭圆于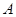 、
、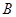 两点,若存在直线使坐标原点
两点,若存在直线使坐标原点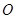 恰好在以
恰好在以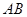 为直径的圆上,则椭圆的离心率取值范围是
为直径的圆上,则椭圆的离心率取值范围是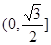
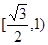
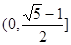
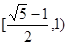
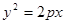 的焦点与双曲线
的焦点与双曲线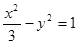 的左焦点重合,则实数
的左焦点重合,则实数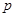 = .
= . 在曲线
在曲线 上,点
上,点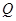 在曲线
在曲线 上,则
上,则 的最小值等于 .
的最小值等于 .