题目内容
16.某水厂的蓄水池中有400吨水,每天零点开始由池中放水向居民供水,同时以每小时60吨的速度向池中注水,若t小时内向居民供水总量为100$\sqrt{6t}$(0≤t≤24),则每天$\frac{25}{6}$点时蓄水池中的存水量最少.分析 根据题意先设t小时后,蓄水池中的存水量为y吨.写出蓄水池中的存水量的函数表达式,再利用换元法求此函数的最小值即得.
解答 解:设t小时后,蓄水池中的存水量为y吨.
则y=400+60t-100$\sqrt{6t}$(0≤t≤24),
设u=$\sqrt{t}$,则u∈[0,2$\sqrt{6}$],y=60u2-100$\sqrt{6}$u+400
∴当u=$\frac{5\sqrt{6}}{6}$即t=$\frac{25}{6}$时,蓄水池中的存水量最少.
故答案为:$\frac{25}{6}$.
点评 本小题主要考查函数模型的选择与应用,解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.属于基础题.

练习册系列答案
相关题目
4.如果满足9x-a≥0>8x-b的实数x的整数值只有1,2,3,那么满足这个条件的整式a,b的有序实数对(a,b)共有( )
| A. | 48对 | B. | 63对 | C. | 64对 | D. | 72对 |
11.直线y=kx+b通过第一、三、四象限,则有( )
| A. | d>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
1.命题p:$\overrightarrow{AB}$•$\overrightarrow{AC}$<0,命题q:∠BAC是钝角.p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知某个车轮旋转的角度α(弧度)与时间t(秒)的函数关系是α=$\frac{2π}{0.64}$t2(t≥0),则车轮启动后第1.6秒时的瞬时角速度是( )
| A. | 20π弧度/秒 | B. | 10π弧度/秒 | C. | 8π弧度/秒 | D. | 5π弧度/秒 |
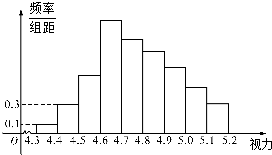 某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.
某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.