题目内容
圆x2+y2-4x-5=0和x2+y2+2y=0的位置关系（ ）
| A．相离 | B．外切 | C．相交 | D．内切 |
把圆x2+y2-4x-5=0和x2+y2+2y=0分别化为标准方程得：
（x-2）2+y2=9，x2+（y+1）2=1，
故圆心坐标分别为（2，0）和（0，-1），半径分别为R=3和r=1，
∵圆心之间的距离d=
=
，R+r=4，R-r=2，
∴R-r＜d＜R+r，
则两圆的位置关系是相交．
故选：C．
（x-2）2+y2=9，x2+（y+1）2=1，
故圆心坐标分别为（2，0）和（0，-1），半径分别为R=3和r=1，
∵圆心之间的距离d=
| (2-0)2+(0+1)2 |
| 5 |
∴R-r＜d＜R+r，
则两圆的位置关系是相交．
故选：C．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
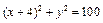相内切，且过点A（4，0），求这个动圆圆心的轨迹方程。