题目内容
【题目】如图所示,在矩形ABCD中,AB=3,BC=4,E,F分别在线段BC,AD上,EF∥AB,将矩形ABEF沿EF折起,记折起后的矩形为MNEF,且平面MNEF⊥平面ECDF.
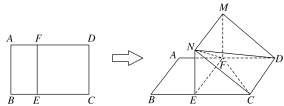
(1)在线段BC是否存在一点E,使得ND⊥FC ,若存在,求出EC的长并证明;
若不存在,请说明理由.
(2)求四面体NEFD体积的最大值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)EC=3时符合;连接ED,交FC于点O,先证明FC⊥平面NED,再证明ND⊥FC.(2) 设NE=x,则FD=EC=4-x,其中0<x<4,再求出![]() ,再利用基本不等式求四面体NEFD体积的最大值.
,再利用基本不等式求四面体NEFD体积的最大值.
(1)证明:EC=3时符合;连接ED,交FC于点O,如图所示.
∵平面MNEF⊥平面ECDF,且NE⊥EF,平面MNEF∩平面ECDF=EF,NE平面MNEF,∴NE⊥平面ECDF.
∵FC平面ECDF,∴FC⊥NE.
∵EC=CD,∴四边形ECDF为正方形,∴FC⊥ED.
又∵ED∩NE=E,ED,NE平面NED,
∴FC⊥平面NED.
∵ND平面NED,∴ND⊥FC.
(2)设NE=x,则FD=EC=4-x,其中0<x<4,
由(1)得NE⊥平面FEC,
∴四面体NEFD的体积为![]() ,
,
所以![]() ,
,
当且仅当x=4-x,即x=2时,四面体NEFD的体积最大,最大值为2

练习册系列答案
相关题目