题目内容
【题目】为了整顿食品的安全卫生，食品监督部门对某食品厂生产的甲、乙两种食品进行了检测调研，检测某种有害微量元素的含量，随机在两种食品中各抽取了10个批次的食品，每个批次各随机地抽取了一件，下表是测量数据的茎叶图（单位：毫克）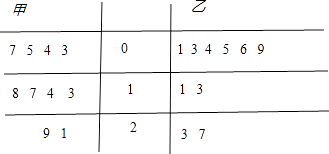 
规定：当食品中的有害微量元素含量在[0，10]时为一等品，在（10，20]为二等品，20以上为劣质品．
（1）用分层抽样的方法在两组数据中各抽取5个数据，再分别从这5个数据中各选取2个．求甲的一等品数与乙的一等品数相等的概率；
（2）每生产一件一等品盈利50元，二等品盈利20元，劣质品亏损20元．根据上表统计得到的甲、乙两种食品为一等品、二等品、劣质品，的频率分别估计这两种食品为，一等品、二等品、劣质品的概率．若分别从甲、乙食品中各抽取l件，设这两件食品给该厂带来的盈利为X，求随机变量X的概率分布和数学期望．
【答案】
（1）解：从甲抽取的5个数据中，一等品有4× 
=2个，非一等品有3个，从乙抽取的5个数据中，一等品有6× =3个，非一等品有2个，
设”从甲中抽取的5个数据中任取2个，一等品个数为i”为事件Ai，（i=0，1，2）则P（A0）= 
= 
，P（A1）= 
= 
，P（A2）= 
= 
，
设”从乙中抽取的5个数据中任取2个，一等品个数为i”为事件Ai，（i=0，1，2）则P（B0）= = ，P（B1）= = ，P（B0）= = ，
∴甲的一等品数与乙的一等品数相等的概率为：
P=P（A2B2）+P（A1B1）+P（A0B0）= 
+ 
+ 
= 
（2）解：由题意，设“从甲中任取一件为一等品”为事件C1，则P（C1）= 
= 
，
设“从甲中任取一件为二等品”为事件C2，则P（C2）= = ，
设“从甲中任取一件劣质品”为事件C3，则P（C3）= 
= 
，
设“从乙中任取一件为一等品”为事件D1，则P（D1）= 
= ，
设“从乙中任取一件为二等品”为事件D2，则P（D2）= = ，
设“从乙中任取一件劣质品”为事件D3，则P（D3）= = ，
X可取﹣40，0，30，40，70，100，
P（X=﹣40）=P（C3D3）= × = 
，
P（X=30）=P（C1D3+C3D1）= 
+ 
= 
= ，
P（X=0）=P（C3D2+C2D3）= × + = 
，
P（X=40）=P（C2D2）= = 
，
P（X=70）=P（C1D2+C2D1）= + 
= 
，
P（X=100）=P（C1D1）= = 
，
∴X的分布列为：
X | ﹣40 | 0 | 30 | 40 | 70 | 100 |
P |
|
|
|
|
|
|
∴E（X）=﹣40× +0× +30× +40× +70× +100× =49.2
【解析】（1）由已知条件，利用互斥事件的概率加法公式能甲的一等品数与乙的一等品数相等的概率概率．（2）随机变量X的所有可能取值为X可取﹣40，0，30，40，70，100，分别求出相对应的概率，由此能求出随机变量X的概率分布和数学期望
【考点精析】本题主要考查了茎叶图和离散型随机变量及其分布列的相关知识点，需要掌握茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少；在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列才能正确解答此题．
