题目内容
【题目】已知椭圆![]() :
:![]() ,该椭圆经过点
,该椭圆经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 是圆
是圆![]() 上任意一点,由
上任意一点,由![]() 引椭圆
引椭圆![]() 的两条切线
的两条切线![]() ,
,![]() ,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
【答案】(1) ![]() .(2)见解析.
.(2)见解析.
【解析】
(1)由椭圆经过点![]() ,可以求出
,可以求出![]() 的值,由离心率为
的值,由离心率为![]() ,可知
,可知![]() 的关系,结合
的关系,结合![]() 之间的,可以求出
之间的,可以求出![]() 的值,这样就求出椭圆的标准方程;
的值,这样就求出椭圆的标准方程;
(2)设![]() ,且
,且![]() .点
.点![]() 引椭圆
引椭圆![]() 的切线方程可设为
的切线方程可设为![]() ,
,
与椭圆方程联立,让根的判断式为零,得到一个关于![]() 的一元二次方程,利用根与系数的关系,可以证明出两条切线斜率的积为定值.
的一元二次方程,利用根与系数的关系,可以证明出两条切线斜率的积为定值.
(1)由题意得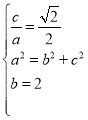 ,解得
,解得![]() ,
,![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() ,且
,且![]() .
.
由题意知,过点![]() 引椭圆
引椭圆![]() 的切线方程可设为
的切线方程可设为![]() ,
,
联立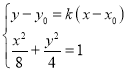 化简得
化简得![]() .
.
∵直线与椭圆相切,
∴![]() ,
,
化简得![]() .
.
∴![]()
![]() .
.
∴两条切线斜率的积为定值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目