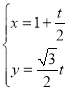题目内容
【题目】已知![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,若
时,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 4x-y-4=0 (2) ![]() .
.
【解析】
(1)a=2时,f(x)=﹣x3+5x2﹣3x﹣1,f(1)=0.f′(x)=﹣3x2+10x﹣3,f′(1)=4.利用点斜式即可得出:函数=f(x)的图象在点(1,f(1))处的切线方程.
(2)g(x)≥f′(x),即(x+1)lnx﹣3x2+x﹣2(a﹣1)≥﹣3x2+(4a+2)x﹣(2a﹣1),化为:4a+1![]() ,(x≥1).令h(x)
,(x≥1).令h(x)![]() ,(x≥1).利用导数研究函数的单调性极值与最值即可得出.
,(x≥1).利用导数研究函数的单调性极值与最值即可得出.
(1)a=2时,![]()
![]()
∴ 函数y=f(x)的图象在点(1,f(1))处的切线方程为:y![]() 0=4(x
0=4(x![]() 1),即4x
1),即4x![]() y
y![]() 4=0
4=0
(2)![]() ,∴
,∴![]() ,
,
化为:![]() .
.
令![]() .
.
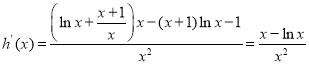 ,
,
令![]()
因此函数![]() 在
在![]() 上单调递增.
上单调递增.
∴ ![]()
∴ ![]()
∴ 函数h(x)在![]() 上单调递增.
上单调递增.
∴ 函数![]() ,
,
∴ ![]() ,解得
,解得![]()
∴ 实数a的取值范围是![]() .
.

【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)有一种植户准备种植该种水果500株,且每株与它“相近”的株数都为![]() ,计划收获后能全部售出,价格为10元
,计划收获后能全部售出,价格为10元![]() ,如果收入(收入=产量×价格)不低于25000元,则
,如果收入(收入=产量×价格)不低于25000元,则![]() 的最大值是多少?
的最大值是多少?
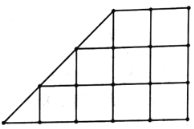
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为![]() ,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: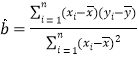 ,
,![]() .
.