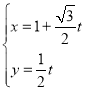题目内容
【题目】已知曲线C的极坐标方程是![]() ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换
,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换 得到曲线E,直线l:
得到曲线E,直线l: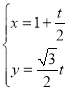 (t为参数)与曲线E交于A,B两点,
(t为参数)与曲线E交于A,B两点,
(1)设曲线C上任一点为![]() ,求
,求![]() 的最小值;
的最小值;
(2)求出曲线E的直角坐标方程,并求出直线l被曲线E截得的弦AB长;
【答案】(1)-2;(2)![]() .
.
【解析】
(1)求出曲线C的参数方程,再代入![]() ,利用辅助角公式求最值即可.
,利用辅助角公式求最值即可.
(2)利用伸缩变换求曲线E的直角坐标方程,再利用直线参数方程中![]() 的几何意义,联立直线与椭圆的方程利用韦达定理求解即可.
的几何意义,联立直线与椭圆的方程利用韦达定理求解即可.
解:(1)根据![]() ,进行化简得C:
,进行化简得C:![]() ,
,
∴曲线C的参数方程![]() (
(![]() 为参数),
为参数),
∴![]() ,
,
则![]() 的最小值为
的最小值为![]() ;
;
(2)∵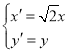 ,∴
,∴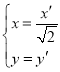 代入C得∴E:
代入C得∴E:![]() ,
,
将直线l的参数方程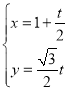 (t为参数),
(t为参数),
代入曲线E方程得:![]() ,
,
∴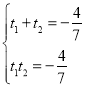 ,
,![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案【题目】如图,将边长为1的正方形ABCD沿x轴正向滚动,先以A为中心顺时针旋转,当B落在x轴时,又以B为中心顺时针旋转,如此下去,设顶点C滚动时的曲线方程为![]() ,则下列说法不正确的是
,则下列说法不正确的是![]()

A.![]() 恒成立B.
恒成立B.![]()
C.![]() D.
D.![]()
【题目】下表列出了10名5至8岁儿童的体重x(单位kg)(这是容易测得的)和体积y(单位dm3)(这是难以测得的),绘制散点图发现,可用线性回归模型拟合y与x的关系:
体重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
体积y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y关于x的线性回归方程![]() (系数精确到0.01);
(系数精确到0.01);
(2)某5岁儿童的体重为13.00kg,估测此儿童的体积.
附注:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,137×14=1918.00.
,137×14=1918.00.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: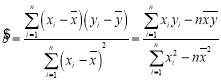 ,
,![]() .
.