题目内容
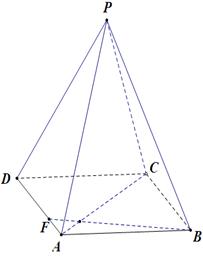
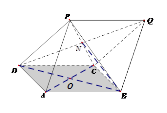
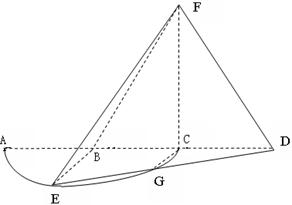
如图,几何体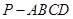 为正四棱锥,几何体
为正四棱锥,几何体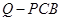 为正四面体.、
为正四面体.、
(1)求证: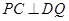 ;
;
(2)求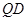 与平面
与平面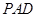 所成角的正弦值.
所成角的正弦值.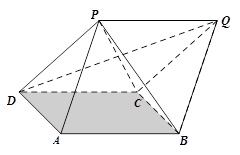
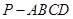 为正四棱锥,几何体
为正四棱锥,几何体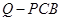 为正四面体.、
为正四面体.、(1)求证:
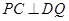 ;
;(2)求
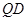 与平面
与平面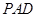 所成角的正弦值.
所成角的正弦值.
解法一:取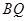 的中点
的中点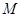 ,连结
,连结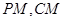 ,由几何体
,由几何体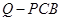 为正四面体得,
为正四面体得,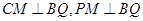 ,所以
,所以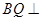 平面
平面 ,从而
,从而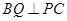 .
.
连结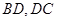 交于点
交于点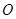 ,连结
,连结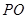 得
得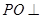 平面
平面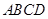 ,
,
 ,所以
,所以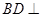 平面
平面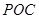 ,从而
,从而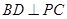 .又
.又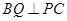
所以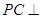 平面
平面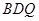 ,从而
,从而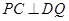 .
.
解法二: 因为几何体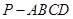 为正四棱锥,几何体
为正四棱锥,几何体 为正四面体.
为正四面体.
故可设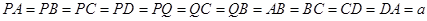
取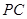 的中点
的中点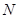 ,连结
,连结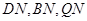 ,由题意知
,由题意知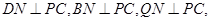
故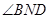 是二面角
是二面角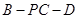 的平面角,
的平面角, 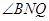 是二面角
是二面角 的平面角,
的平面角,
在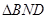 中,
中,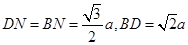 ,
,
所以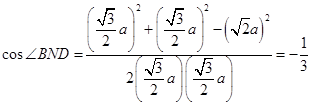 ,
,
在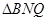 中,
中,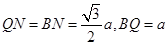 ,
,
所以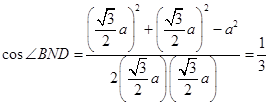
从而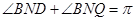 ,从而
,从而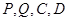 四点共面,
四点共面,
故四边形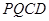 为菱形,从而
为菱形,从而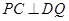
(2)由解法二知四边形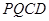 为菱形,于是
为菱形,于是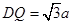 ,
,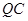 ∥
∥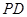 ,
,
所以点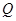 到平面
到平面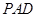 的距离等于点
的距离等于点 到平面
到平面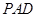 的距离,
的距离,
设点 到平面
到平面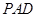 的距离为
的距离为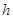 ,由
,由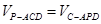 得:
得: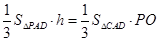
进而得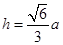 ,所以
,所以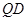 与平面
与平面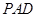 所成角的正弦值
所成角的正弦值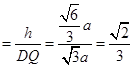
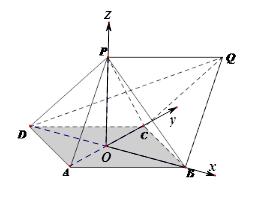
解法三:如图,以OB为x轴,OC为y轴,OP为z轴建立空间直角坐标系。
不妨设|OB|=1,则B(1,0,0),C(0,1,0), D(-1,0,0),A(0,-1,0)
因为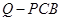 为正四面体,所以
为正四面体,所以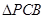 为正三角形,所以
为正三角形,所以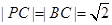 ,所以
,所以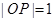 ,因此P(0,0,1)。
,因此P(0,0,1)。
设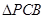 的重心为M,则
的重心为M,则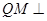 面PCB,又
面PCB,又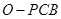 也为正三棱锥,因此
也为正三棱锥,因此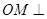 面PCB,因此O、M、Q三点共线,所以OQ垂直面PCB,即
面PCB,因此O、M、Q三点共线,所以OQ垂直面PCB,即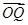 是平面PCB的一个法向量,
是平面PCB的一个法向量,
由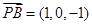 ,
,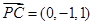 易得平面PCB的一个法向量可以取
易得平面PCB的一个法向量可以取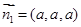 ,所以不妨设Q(a,a,a),则
,所以不妨设Q(a,a,a),则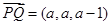 ,因为
,因为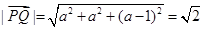 解得a=1,所以Q(1,1,1)。
解得a=1,所以Q(1,1,1)。
(1)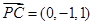 ,
,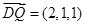 ,
,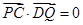 ,所以
,所以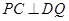 ;
;
(2)设面PAD的一个法向量为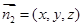 ,
,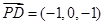 ,
,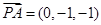 ,由
,由
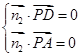 解得一个法向量
解得一个法向量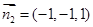 ,
,
所以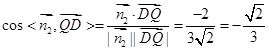 ,所以QD与平面PAD所成角的正弦值为
,所以QD与平面PAD所成角的正弦值为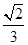 。
。
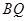 的中点
的中点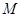 ,连结
,连结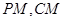 ,由几何体
,由几何体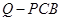 为正四面体得,
为正四面体得,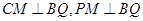 ,所以
,所以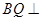 平面
平面 ,从而
,从而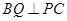 .
.连结
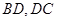 交于点
交于点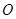 ,连结
,连结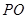 得
得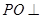 平面
平面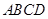 ,
, ,所以
,所以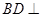 平面
平面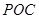 ,从而
,从而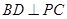 .又
.又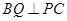
所以
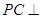 平面
平面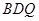 ,从而
,从而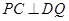 .
.解法二: 因为几何体
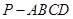 为正四棱锥,几何体
为正四棱锥,几何体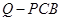 为正四面体.
为正四面体.
故可设
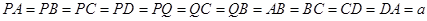
取
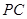 的中点
的中点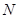 ,连结
,连结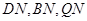 ,由题意知
,由题意知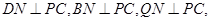
故
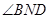 是二面角
是二面角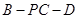 的平面角,
的平面角, 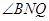 是二面角
是二面角 的平面角,
的平面角,在
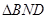 中,
中,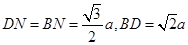 ,
,所以
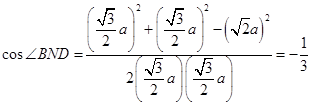 ,
,在
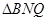 中,
中,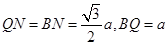 ,
,所以
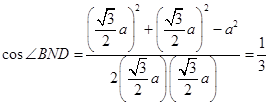
从而
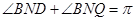 ,从而
,从而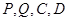 四点共面,
四点共面,故四边形
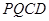 为菱形,从而
为菱形,从而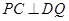
(2)由解法二知四边形
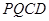 为菱形,于是
为菱形,于是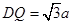 ,
,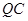 ∥
∥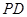 ,
,所以点
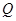 到平面
到平面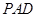 的距离等于点
的距离等于点 到平面
到平面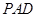 的距离,
的距离,设点
 到平面
到平面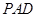 的距离为
的距离为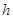 ,由
,由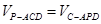 得:
得: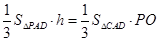
进而得
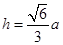 ,所以
,所以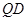 与平面
与平面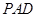 所成角的正弦值
所成角的正弦值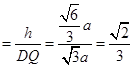
解法三:如图,以OB为x轴,OC为y轴,OP为z轴建立空间直角坐标系。
不妨设|OB|=1,则B(1,0,0),C(0,1,0), D(-1,0,0),A(0,-1,0)

因为
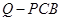 为正四面体,所以
为正四面体,所以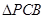 为正三角形,所以
为正三角形,所以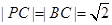 ,所以
,所以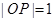 ,因此P(0,0,1)。
,因此P(0,0,1)。设
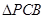 的重心为M,则
的重心为M,则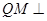 面PCB,又
面PCB,又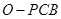 也为正三棱锥,因此
也为正三棱锥,因此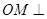 面PCB,因此O、M、Q三点共线,所以OQ垂直面PCB,即
面PCB,因此O、M、Q三点共线,所以OQ垂直面PCB,即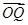 是平面PCB的一个法向量,
是平面PCB的一个法向量,由
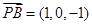 ,
,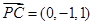 易得平面PCB的一个法向量可以取
易得平面PCB的一个法向量可以取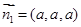 ,所以不妨设Q(a,a,a),则
,所以不妨设Q(a,a,a),则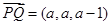 ,因为
,因为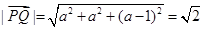 解得a=1,所以Q(1,1,1)。
解得a=1,所以Q(1,1,1)。(1)
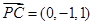 ,
,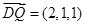 ,
,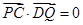 ,所以
,所以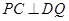 ;
;(2)设面PAD的一个法向量为
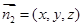 ,
,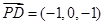 ,
,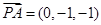 ,由
,由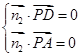 解得一个法向量
解得一个法向量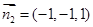 ,
,所以
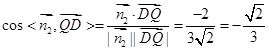 ,所以QD与平面PAD所成角的正弦值为
,所以QD与平面PAD所成角的正弦值为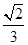 。
。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
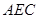 是半径为
是半径为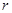 的半圆,
的半圆,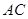 为直径,点
为直径,点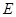 为弧
为弧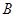 和点
和点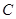 为线段
为线段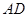 的三等分点,线段
的三等分点,线段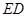 与弧
与弧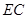 交于点
交于点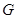 ,且
,且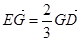 ,平面
,平面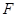 满足
满足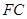
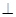 平面
平面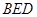 ,
,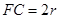 。
。
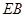
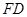 ;
; (及其内部)绕
(及其内部)绕 ,
, 所成的角为
所成的角为 ,且
,且 =( )
=( )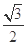


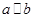 ,a与c的夹角为
,a与c的夹角为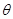 ,那么b与c的夹角为( )
,那么b与c的夹角为( )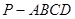 中,
中,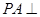 平面
平面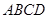 ,
,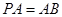
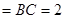 ,
,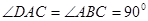 ,
,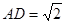 .
.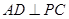 ;
;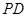 与平面
与平面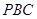 所成角的大小.
所成角的大小.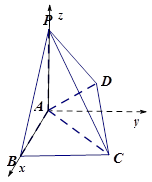
 ,
,
 ,则二面角
,则二面角 的大小( )
的大小( )
 中,AB=1,侧棱
中,AB=1,侧棱 与底面
与底面 所成角的正切值为
所成角的正切值为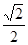 .
.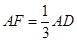 ,求点A到平面PB
,求点A到平面PB F的距离.
F的距离.